单选题 (共 10 题 ),每题只有一个选项正确
设函数 $f(x, y)$ 连续, 则二次积分 $\int_{\frac{\pi}{2}}^\pi d x \int_{\sin x}^1 f(x, y) d y$ 等于
$\text{A.}$ $\int_0^1 d y \int_{\pi+\arcsin y}^\pi f(x, y) d x$.
$\text{B.}$ $\int_0^1 d y \int_{\pi-\arcsin y}^\pi f(x, y) d x$.
$\text{C.}$ $\int_0^1 d y \int_{\frac{\pi}{2}}^{x+\arcsin y} f(x, y) d x$.
$\text{D.}$ $\int_0^1 d y \int_{\frac{\pi}{2}}^{\pi a r c s i n y} f(x, y) d x$.
设函数 $f(x, y)$ 连续, 则 $\int_1^2 d x \int_x^2 f(x, y) d y+\int_1^2 d y \int_y^{4-y} f(x, y) d x=$
$\text{A.}$ $\int_1^2 d x \int_1^{4-x} f(x, y) d y$.
$\text{B.}$ $\int_1^2 d x \int_x^{4-x} f(x, y) d y$.
$\text{C.}$ $\int_1^2 d y \int_1^{4-y} f(x, y) d x$.
$\text{D.}$ $\int_1^2 d y \int_y^2 f(x, y) d x$.
累次积分 $\int_0^{\frac{\pi}{2}} d \theta \int_0^{\cos \theta} f(r \cos \theta, r \sin \theta) r d r$ 可以写成
$\text{A.}$ $\int_0^1 d y \int_0^{\sqrt{y-y^2}} f(x, y) d x$.
$\text{B.}$ $\int_0^1 d y \int_0^{\sqrt{1-y^2}} f(x, y) d x$.
$\text{C.}$ $\int_0^1 d x \int_0^1 f(x, y) d y$.
$\text{D.}$ $\int_0^1 d x \int_0^{\sqrt{x-x^2}} f(x, y) d y$.
设 $D$ 是第一象限中曲线 $2 x y=1,4 x y=1$ 与直线 $y=x, y=\sqrt{3} x$ 围成的平面区域, 函数 $f(x, y)$ 在 $D$ 上连续, 则 $\iint_D f(x, y) d x d y=$
$\text{A.}$ $\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{2 \sin ^2 \theta}}^{\frac{1}{\sin ^2 \theta}} f(r \cos \theta, r \sin \theta) r d r$.
$\text{B.}$ $\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{1}{\sqrt{\sin 2 \theta}}} f(r \cos \theta, r \sin \theta) r d r$.
$\text{C.}$ $\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{2 \sin 2 \theta}}^{\frac{1}{\sin ^2 \theta}} f(r \cos \theta, r \sin \theta) d r$.
$\text{D.}$ $\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{2 \sin ^2 \theta}}}^{\frac{1}{\sqrt{\sin ^2 \theta}}} f(r \cos \theta, r \sin \theta) d r$.
设 $f(x, y)$ 为连续函数, 则 $\int_0^{\frac{1}{4}} d \theta \int_0^1 f(r \cos \theta, r \sin \theta) r d r$ 等于
$\text{A.}$ $\int_0^{\frac{\sqrt{2}}{2}} d x \int_x^{\sqrt{1-x^x}} f(x, y) d y$.
$\text{B.}$ $\int_0^{\frac{\sqrt{2}}{2}} d x \int_0^{\sqrt{1-x^2}} f(x, y) d y$.
$\text{C.}$ $\int_0^{\frac{\sqrt{2}}{2}} d y \int_y^{\sqrt{1-y^2}} f(x, y) d x$.
$\text{D.}$ $\int_0^{\frac{\sqrt{2}}{2}} d y \int_0^{\sqrt{1-y^2}} f(x, y) d x$.
设 $I_1=\iint_D \cos \sqrt{x^2+y^2} d \sigma, I_2=\iint_D \cos \left(x^2+y^2\right) d \sigma, I_3=\iint_D \cos \left(x^2+y^2\right)^2 d d$ 其中$D=\left\{(x, y) \mid x^2+y^2 \leqslant 1\right\}$, 则
$\text{A.}$ $I_3>I_2>I_1$.
$\text{B.}$ $I_1>I_2>I_3$.
$\text{C.}$ $I_2>I_1>I_3$.
$\text{D.}$ $I_3>I_1>I_2$.
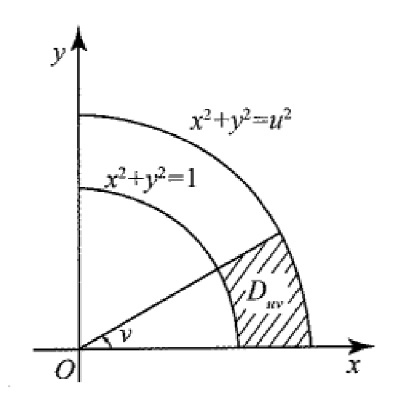
设函数 $f(x)$ 连续, 若 $F(u, v)=\iint_{D_{ v }} \frac{f\left(x^2+y^2\right)}{\sqrt{x^2+y^2}} d x d y$,其中区域 $D_{ uv }$ 为图中阴影部分, 则 $\frac{\partial F}{\partial u}=$
$\text{A.}$ $v f\left(u^2\right)$.
$\text{B.}$ $\frac{v}{u} f\left(u^2\right)$.
$\text{C.}$ $v f(u)$.
$\text{D.}$ $\frac{v}{u} f(u)$.
设 $f(x, y)$ 连续, 且 $f(x, y)=x y+\iint_D f(u, v) d u d v$, 其中 $D$ 是由 $y=0, y=x^2, x=1$所围成的区域,则 $f(x, y)$ 等于
$\text{A.}$ $x y$.
$\text{B.}$ $2 x y$.
$\text{C.}$ $x y+\frac{1}{8}$.
$\text{D.}$ $x y+1$.
设 $D_k$ 是圆域 $D=\left\{(x, y) \mid x^2+y^2 \leqslant 1\right\}$ 在第 $k$ 象限的部分, 记 $I_k=\iint_{D_k}(y-x) d x d y(k=$ $1,2,3,4)$, 则
$\text{A.}$ $I_1>0$.
$\text{B.}$ $I_2>0$.
$\text{C.}$ $I_3>0$.
$\text{D.}$ $I_4>0$.
设 $D$ 是 $x O y$ 平面上以 $(1,1),(-1,1)$ 和 $(-1,-1)$ 为顶点的三角形区域, $D_1$是 $D$ 在第一象限的部分, 则 $\iint_D(x y+\cos x \sin y) d x d y$ 等于
$\text{A.}$ $2 \iint_{D_1} \cos x \sin y d x d y$.
$\text{B.}$ $2 \iint_{D_1} x y d x d y$.
$\text{C.}$ $4 \iint_{D_1}(x y+\cos x \sin y) d x d y$.
$\text{D.}$ 0 .