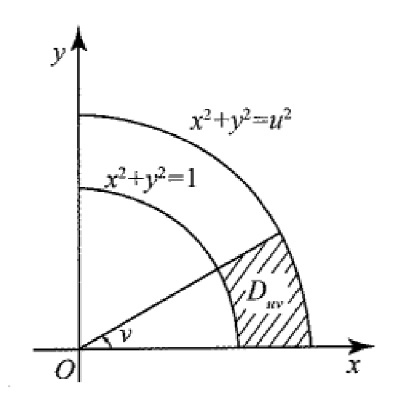
设函数 $f(x)$ 连续, 若 $F(u, v)=\iint_{D_{ v }} \frac{f\left(x^2+y^2\right)}{\sqrt{x^2+y^2}} d x d y$,其中区域 $D_{ uv }$ 为图中阴影部分, 则 $\frac{\partial F}{\partial u}=$
A
$v f\left(u^2\right)$.
B
$\frac{v}{u} f\left(u^2\right)$.
C
$v f(u)$.
D
$\frac{v}{u} f(u)$.
E
F