单选题 (共 10 题 ),每题只有一个选项正确
设 $\Omega$ 是有由曲面 $z=x^2+y^2 , \quad y=x , \quad y=0 , \quad z=1$ 在第一卦限所围成的区域, $f(x, y, z)$在 $\Omega$ 上连续,则 $\iiint_{\Omega} f(x, y, z) d v$ 等于
$\text{A.}$ $\int_0^1 d y \int_y^{\sqrt{1-y^2}} d x \int_{x^2+y^2}^1 f(x, y, z) d z$
$\text{B.}$ $\quad \int_0^{\frac{\sqrt{2}}{2}} d x \int_y^{\sqrt{1-y^2}} d y \int_{x^2+y^2}^1 f(x, y, z) d z$
$\text{C.}$ $\int_0^{\frac{\sqrt{2}}{2}} d y \int_y^{\sqrt{1-y^2}} d x \int_0^1 f(x, y, z) d z$
$\text{D.}$ $\int_0^{\frac{\sqrt{2}}{2}} d y \int_y^{\sqrt{1-y^2}} d x \int_{x^2+y^2}^1 f(x, y, z) d z$
设直线 $L:\left\{\begin{array}{l}x+3 y+2 z+5=0 \\ 2 x-y-10 z-12=0\end{array}\right.$ 及平面 $\pi: \quad 4 x-2 y+z-6=0$, 则直线 $L$
$\text{A.}$ 平行于平面 $\pi$.
$\text{B.}$ 在平面 $\pi$ 上.
$\text{C.}$ 垂直于平面 $\pi$.
$\text{D.}$ 垂平面 $\pi$ 斜交.
设空间区域 $\Omega_1: x^2+y^2+z^2 \leq R^2, z \geq 0 ; \quad \Omega_2: x^2+y^2+z^2 \leq R^2, x \geq 0, y \geq 0, z \geq 0$, 则
$\text{A.}$ $\iiint_{\Omega_1} x d V=4 \iiint_{\Omega_2} x d V$.
$\text{B.}$ $\iiint_{\Omega_1} y d V=4 \iiint_{\Omega_2} y d V$.
$\text{C.}$ $\iiint_{\Omega_1} z d V=4 \iiint_{\Omega_2} z d V$.
$\text{D.}$ $\iiint_{\Omega_1} x y z d V=4 \iiint_{\Omega_2} x y z d V$.
设直线 $l_1: \frac{x-3}{2}=\frac{y}{1}=\frac{z-1}{0}, l_2: \frac{x+1}{1}=\frac{y-2}{0}=\frac{z}{1}$.则 $l_1$ 与 $l_2 $
$\text{A.}$ 平行
$\text{B.}$ 垂直
$\text{C.}$ 相交但不垂直.
$\text{D.}$ 异面
下列四个曲线积分中,在区域 $0 < x^2+y^2 < +\infty$ 上路径无关的是
$\text{A.}$ $\int_C \frac{y d x-x d y}{x^2+y^2}$.
$\text{B.}$ $\int_C \frac{(x-y) d x+(x+y) d y}{x^2+y^2}$.
$\text{C.}$ $\int_C \frac{x d y-y d x}{4 x^2+y^2}$.
$\text{D.}$ $\int_C \frac{x d x+y d y}{x^2+y^2}$
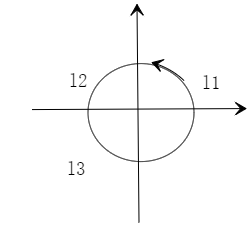
设曲线 $L$ 为 $x^2+y^2=1$, 取逆时针方向, $f(x, y)>0, f(x,-y)=f(x, y) \cdot L_1, L_2, L_3$ ,如图所示,记 $I_1=\int_{L_1} f(x, y) d x, I_2=\int_{L_2} f(x, y) d s, \quad I_3=\int_{L_3} f(x, y) d x$ ,则
$\text{A.}$ $I_1>I_2>I_3$
$\text{B.}$ $ I_2>I_3>I_1$.
$\text{C.}$ $ I_3>I_2>I_1$
$\text{D.}$ $I_2>I_1>I_3$
设 $f(x)$ 有连续的导数, $f(0)=0$ ,区域 $\Omega$ 由柱面 $x^2+y^2=t^2 \quad(t>0)$ 和两平面 $z=0$ , $z=1$ 所围成,则 $\lim _{t \rightarrow 0^{+}} \frac{\iiint_{\Omega} f\left(x^2+y^2\right) d v}{t^4}$ 等于
$\text{A.}$ $\pi f^{\prime}(0)$
$\text{B.}$ $\pi f(0)$.
$\text{C.}$ $\frac{\pi}{2} f(0)$
$\text{D.}$ $\frac{\pi}{2} f^{\prime}(0)$
曲线 $\Gamma:\left\{\begin{array}{l}\frac{x^2}{16}+\frac{y^2}{4}-\frac{z^2}{5}=1 \\ x-2 z+3=0\end{array}\right.$, 在 $x O y$ 平面上的投影曲线的方程是
$\text{A.}$ $x^2+20 y^2-24 x-116=0$.
$\text{B.}$ $4 y^2+4 z^2-12 z-7=0$.
$\text{C.}$ $\left\{\begin{array}{l}x^2+20 y^2-24 x-116=0 \\ z=0\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}4 y^2+4 z^2-12 z-7=0 \\ x=0\end{array}\right.$
设 $L$ 为由 $y^2=x+3$ 及 $x=2$ 围成的区域的边界, 取逆时针方向, 则 $\oint_L \frac{x d y-y d x}{x^2+y^2}$ 等于
$\text{A.}$ $-2 \pi$.
$\text{B.}$ $ 2 \pi$.
$\text{C.}$ $\pi$.
$\text{D.}$ 0
设 $L: y=\sqrt{1-x^2}$ 从点 $A(-1,0)$ 到点 $B(1,0)$, 则 $\int_L 2 x d y-\sqrt{x^2+y^2} d x=$
$\text{A.}$ $ \pi+2$.
$\text{B.}$ $ \pi-2$.
$\text{C.}$ $-\pi-2$.
$\text{D.}$ $-\pi+2$.