单选题 (共 6 题 ),每题只有一个选项正确
设函数 $f(x)=x^4+\left|x^3\right|$, 则使 $f^{(n)}(0)$ 存在的最高阶数 $n=(\quad)$.
$\text{A.}$ 1 ;
$\text{B.}$ 2 ;
$\text{C.}$ 3 ;
$\text{D.}$ 4.
若 $F(x)=\int_0^x(2 t-x) f(t) d t$, 其中 $f(x)$ 在区间上 $(-1,1)$ 二阶可导且 $f ^{\prime}( x )>0$, 则 ( ).
$\text{A.}$ 函数 $F(x)$ 必在 $x=0$ 处取得极大值;
$\text{B.}$ 函数 $F(x)$ 必在 $x=0$ 处取得极小值;
$\text{C.}$ 函数 $F(x)$ 在 $x=0$ 处没有极值, 但点 $(0, F(0))$ 为曲线 $y=F(x)$ 的拐点;
$\text{D.}$ 函数 $F(x)$ 在 $x=0$ 处没有极值, 点 $(0, F(0))$ 也不是曲线 $y=F(x)$ 的拐点。
函数 $f(x)=x e^x$ 的带有皮亚诺型余项的 $n$ 阶麦克劳林公式为 ( ).
$\text{A.}$ $x e^x=x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+o\left(x^n\right)$
$\text{B.}$ $x e^x=x+x^2+\frac{x^3}{2!}+\cdots+\frac{x^n}{(n-1)!}+o\left(x^n\right)$
$\text{C.}$ $x e^x=x+\frac{x^2}{2}+\cdots+\frac{x^n}{n}+o\left(x^n\right)$
$\text{D.}$ $x e^x=x+x^2+\frac{x^3}{2}+\cdots+\frac{x^n}{n-1}+o\left(x^n\right)$
设函数 $f_i(x)(i=1,2)$ 具有二阶连续导数, 且 $f_i^{\prime \prime}\left(x_0\right) < 0(i=1,2)$.若两条曲线 $y=f_i(x)(i=1,2)$ 在点 $\left(x_0, y_0\right)$ 处具有公切线 $y=g(x)$, 且该点处曲线 $y=f_1(x)$ 的曲率大于曲线 $y=f_2(x)$ 的曲率, 则在 $x_0$ 的某个邻域内 ,有 ( )
$\text{A.}$ $f_1(x) \leq f_2(x) \leq g(x)$.
$\text{B.}$ $f_2(x) \leq f_1(x) \leq g(x)$.
$\text{C.}$ $f_1(x) \leq g(x) \leq f_2(x)$.
$\text{D.}$ $f_2(x) \leq g(x) \leq f_1(x)$.
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续, 其导函数的图形如图所示, 则
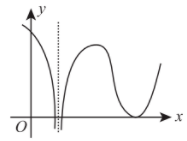
$\text{A.}$ 函数 $f(x)$ 有 2 个极值点, 曲线 $y=f(x)$ 有 2 个拐点.
$\text{B.}$ 函数 $f(x)$ 有 2 个极值点, 曲线 $y=f(x)$ 有 3 个拐点.
$\text{C.}$ 函数 $f(x)$ 有 3 个极值点, 曲线 $y=f(x)$ 有 1 个拐点.
$\text{D.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 2 个拐点.
已知函数 $f(x)=\int_0^x e ^{t^2} \sin t d t, g(x)=\int_0^x e ^{t^2} d t \cdot \sin ^2 x$ ,则 ( ).
$\text{A.}$ $x=0$ 是 $f(x)$ 的极值点,也是 $g(x)$ 的极值点
$\text{B.}$ $x=0$ 是 $f(x)$ 的极值点, $(0,0)$ 是曲线 $y=g(x)$ 的拐点
$\text{C.}$ $(0,0)$ 是 $y=f(x)$ 的拐点, $x=0$ 是 $g(x)$ 的极值点
$\text{D.}$ $(0,0)$ 是曲线 $y=f(x)$ 的拐点,也是曲线 $y=g(x)$ 的拐点