单选题 （共 6 题 ），每题只有一个选项正确
设 n 阶方阵 $A$ 不可逆，则必有
$\text{A.}$ 秩 $( A ) < n$
$\text{B.}$ 秩 $( A )=n-1$
$\text{C.}$ $A=0$
$\text{D.}$ 方程组 $A x =0$ 只有零解
设 $A$ 为 $n$ 阶可逆方阵, $k$ 为非零常数,则有 ( ).
$\text{A.}$ $(k A )^{-1}=k A ^{-1}$
$\text{B.}$ $(k A )^{ T }=k A ^{ T }$
$\text{C.}$ $|k A |=k| A |$
$\text{D.}$ $(k A )^*=k A ^*$
设 $D=\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|, A_{i j}$ 为 $D$ 的 $(i, j)$ 元的代数余子式，则 $A_{31}+2 A_{32}+3 A_{33}=$
$\text{A.}$ $\left|\begin{array}{ccc}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 1 & 2 & 3\end{array}\right|$
$\text{B.}$ $\left|\begin{array}{ccc}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 1 & -2 & 3\end{array}\right|$
$\text{C.}$ $\left|\begin{array}{lll}a_{11} & a_{12} & 1 \\ a_{21} & a_{22} & 2 \\ a_{31} & a_{32} & 3\end{array}\right|$
$\text{D.}$ $\left|\begin{array}{llc}a_{11} & a_{12} & 1 \\ a_{21} & a_{22} & -2 \\ a_{31} & a_{32} & 3\end{array}\right|$
三元一次方程组
$$
\left\{\begin{array}{l}
x_1+x_2+a x_3=4 \\
x_1-x_2+2 x_3=-4 \\
-x_1+a x_2+x_3=a^2
\end{array}\right.
$$
所代表的三平面不可能的位置关系为
$\text{A.}$ 
$\text{B.}$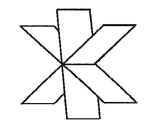 
$\text{C.}$ 
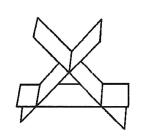$\text{D.}$ 
下列矩阵中是正定矩阵的为（ ）
$\text{A.}$ $\left(\begin{array}{ll}2 & 3 \\ 3 & 4\end{array}\right)$
$\text{B.}$ $\left(\begin{array}{ll}3 & 4 \\ 2 & 6\end{array}\right)$
$\text{C.}$ $\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & 2 & -3 \\ 0 & -3 & 5\end{array}\right)$
$\text{D.}$ $\left(\begin{array}{lll}1 & 1 & 1 \\ 1 & 2 & 0 \\ 1 & 0 & 2\end{array}\right)$
设矩阵 $A=\left(\begin{array}{lll}a & b & b \\ b & a & b \\ b & b & a\end{array}\right) ， B=\left(\begin{array}{lll}b & b & a \\ b & a & b \\ a & b & b\end{array}\right) ， C=\left(\begin{array}{lll}b & a & b \\ a & b & b \\ b & b & a\end{array}\right) ， A ， B ， C$ 均可逆，则（）
$\text{A.}$ $A, B$ 不相似但合同.
$\text{B.}$ $B ， C$ 既相似又合同.
$\text{C.}$ $A, C$ 不相似但合同.
$\text{D.}$ $B, C$ 不相似但合同.