单选题 (共 4 题 ),每题只有一个选项正确
将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )

$\text{A.}$ 等腰三角形
$\text{B.}$ 直角三角形
$\text{C.}$ 矩形
$\text{D.}$ 菱形
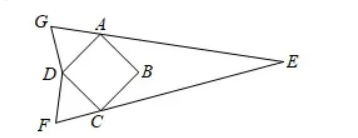
如图, 分别以正方形 $A B C D$ 的两条边 $A D 、 C D$ 为边向外作两个正三角形, 即 $\triangle A D G$ 与 $\triangle C$ $D F$, 然后延长 $G A, F C$ 交于点 $E$, 得到一个 “镖型” $A B C E$. 已知正方形 $A B C D$ 的边长为 2 , 则 “镖 型” $A B C E$ 的周长为
$\text{A.}$ $8+\sqrt{10}$
$\text{B.}$ $4+4 \sqrt{5}$
$\text{C.}$ $4+4 \sqrt{3}$
$\text{D.}$ $8+4 \sqrt{3}$
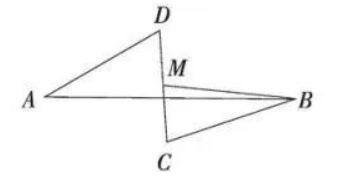
在一平面内, 线段 $A B=8$, 线段 $B C=C D=D A=4$, 将四条线段首尾顺次相接, 把 $A B$ 固定, 当 $A D$ 绕点 $A$ 从 $A B$ 开始逆时针旋转到某一位置时, $B C, C D$ 将 会跟随出现到相应的位置 (如图), 取线段 $C D$ 的中点 $M$, 转 动过程中点 $M$ 与点 $B$ 距离不可能是
$\text{A.}$ 3
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 8
填空题 (共 2 题 ),请把答案直接填写在答题纸上
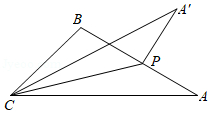
如图, 在 $\triangle A B C$ 中, $\angle B A C=30^{\circ}, \angle A C B=45^{\circ}, A B=2$, 点 $P$ 从点 $A$ 出发沿 $A B$ 方向运动, 到达点 $B$ 时停止运动, 连结 $C P$, 点 $A$ 关于直线 $C P$ 的对称点为 $A^{\prime}$, 连结 $A^{\prime} C, A^{\prime} P$. 在运 动过程中, 点 $A^{\prime}$ 到直线 $A B$ 距离的最大值是 ( ) ; 点 $P$ 到达点 $B$ 时, 线段 $A^{\prime} P$ 扫过的面积 为 ( )
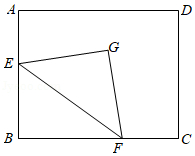
如图, 在矩形 $A B C D$ 中, $A B=4, A D=5$, 点 $E, F$ 分别是边 $A B$, $B C$ 上的动点, 点 $E$ 不与 $A, B$ 重合, 且 $E F=A B, G$ 是五边形 $A E F C D$ 内满足 $G E=G F$ 且 $\angle E G F=90^{\circ}$ 的点. 现给出以下结论:
(1) $\angle G E B$ 与 $\angle G F B$ 一定互补;
(2)点 $G$ 到边 $A B, B C$ 的距离一定相等;
(3)点 $G$ 到边 $A D, D C$ 的距离可能相等;
(4) 点 $G$ 到边 $A B$ 的距离的最大值为 $2 \sqrt{2}$.
其中正确的是 ( )