单选题 （共 10 题 ），每题只有一个选项正确
已知 $a>b, c$ 为任意实数, 则下列不等式中总是成立的是
$\text{A.}$ $a+c < b+c$
$\text{B.}$ $a c>b c$
$\text{C.}$ $a-c>b-c$
$\text{D.}$ $a c < b c$
已知实数 $a, b, c$ 在数轴上对应的点如图所示, 则下列关系中, 正确的是
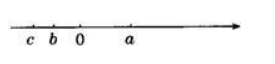
$\text{A.}$ $a b>b c$
$\text{B.}$ $a c>a b$
$\text{C.}$ $a b < b c$
$\text{D.}$ $c+b>a+b$
已知 $a < b$, 下列式子不一定成立的是
$\text{A.}$ $a-1 < b-1$
$\text{B.}$ $-2 a>-2 b$
$\text{C.}$ $a+1 < b+1$
$\text{D.}$ $m a>m b$
若 $2 a+3>2 b+3$, 则下列不等式中错误的是
$\text{A.}$ $-\frac{a}{5} < -\frac{b}{5}$
$\text{B.}$ $-2 a>-2 b$
$\text{C.}$ $a-2>b-2$
$\text{D.}$ $-(-a)>-(-b)$
若 $a>b, c < 0$, 则下列四个不等式中成立的是
$\text{A.}$ $a c>b c$
$\text{B.}$ $\frac{a}{c} < \frac{b}{c}$
$\text{C.}$ $a-c < b-c$
$\text{D.}$ $a+c < b+c$
设 $a 、 b 、 c$ 表示三种不同物体的质量, 用天平称两次, 情况如图所示, 则这三种物体的质量从小到大排序正确的是
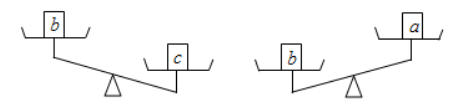
$\text{A.}$ $c < b < a$
$\text{B.}$ $b < a < c$
$\text{C.}$ $c < a < b$
$\text{D.}$ $a < b < c$
如果 $t>0$, 那么 $a+t$ 与 $a$ 的大小关系是
$\text{A.}$ $a+t>a$
$\text{B.}$ $a+t < a$
$\text{C.}$ $a+t \geq a$
$\text{D.}$ 不能确定
已知实数 $a, b$ 满足 $a>b-1$, 则
$\text{A.}$ $a>b$
$\text{B.}$ $b>a$
$\text{C.}$ $a+2>b+1$
$\text{D.}$ $b+1>a+2$
已知关于 $x$ 的不等式 $(2-a) x>3$ 的解集为 $x < \frac{3}{2-a}$, 则 $a$ 的取值范围是
$\text{A.}$ $a>0$
$\text{B.}$ $a < 0$
$\text{C.}$ $a>2$
$\text{D.}$ $a < 2$
已知三角形三边的长分别为 $1 、 2 、 x$, 则 $x$ 的取值范围在数轴上表示为
$\text{A.}$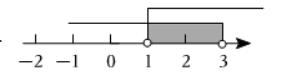 
$\text{B.}$ 
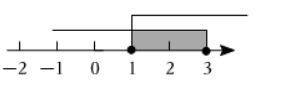$\text{C.}$ 
$\text{D.}$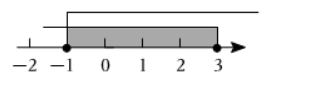 
填空题 （共 3 题 ），请把答案直接填写在答题纸上
不等式 $-5 x \geq-13$ 的解集中, 最大的整数解是
我们用 $[a]$ 表示不大于 $a$ 的最大整数, 例如: $[1.5]=1,[-2.3]=-3$. 若 $[x]+3=1$, 则 $x$ 的取值范围是
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
阅读下列材料:
解答 “已知 $x-y=2$, 且 $x>1, y < 0$, 试确定 $x+y$ 的取值范围”有如下解法:
解: $\because x-y=2, \therefore x=y+2$,
又 $\because x>1$,
$$
\begin{aligned}
& \therefore y+2>1, \\
& \therefore y>-1, \\
& \text { 又 } \because y < 0,-1 < y < 0 \text { (1), }
\end{aligned}
$$
同理得: $1 < x < 2(2)$,
由(1) + (2)得 $-1+1 < y+x < 0+2$,
$\therefore x+y$ 的取值范围是 $0 < x+y < 2$.
请按照上述方法, 完成下列问题.
(1) 已知 $x-y=3$, 且 $x>2, y < 1$, 则 $x+y$ 的取值范围是
(2) 已知 $y>1, x < -1$, 若 $x-y=a$ 成立, 求 $x-2 y$ 的取值范围. (结果用含 $a$ 的式子表示)
比较 $a+b$ 与 $a-b$ 的大小时, 我们可以采用下列解法:
解: $\because(a+b)-(a-b)=a+b-a+b=2 b$,
当 $2 b>0$, 即 $b>0$ 时, $a+b>a-b$ ；
当 $2 b < 0$, 即 $b < 0$ 时, $a+b < a-b$ ；
当 $2 b=0$, 即 $b=0$ 时, $a+b=a-b$.
这种比较大小的方法叫“作差法”, 请用“作差法”比较 $x^2-x+1$ 与 $x^2+2 x+1$ 的大小.
如果字母 $a$ 是有理数, 请比较 $a$ 与 $\frac{1}{a}$ 的大小.
阅读与思考:
(1) 若 $x < 2$. 则 $x-2$ ________ 0, 依据是 ________
若 $x>-3$, 则 $x+3$ ________ 0 , 依据是 ________
若 $x>-3$. 则 $3 x$ ________ -9 , 依据是 ________
若 $x < 2$, 则 $-2 x$ ________ -4 , 依据是 ________
(2) 根据 (1) 的启示, 若 $-3 < x < 2$ 时. 请你化简 $|x-2|+|x+3|-|3 x+9|-|4-2 x|$.
某商店先在广州以每件 15 元的价格购进某种商品 10 件, 后来又到深圳以每件 12.5 元的价格购进同一种商品 40 件. 如果商店销售这些商品时, 每件定价为 $x$ 元, 可获得大于 $12 \%$ 的利润, 用不等式表示问题中的不等关系, 并检验 $x=14$ (元) 是否使不等式成立?
解不等式并在数轴上表示此不等式解集: $\frac{2-x}{2}>1-\frac{3-x}{4}$.
(1) 不等式 $x < \frac{7}{2}$ 有多少个解? 请找出几个.
(2) 不等式 $x < \frac{7}{2}$ 有多少个正整数解? 请一一写出.
定义：对于实数 $a$, 符号 $[a]$ 表示不大于 $a$ 的最大整数. 例如： $[5.7]=5,[5]=5,[-3.14]=-4$. 如果 $[a]=-2$. 那么请你找出几个 $a$的值.