大学物理习题集

导出试卷

大学物理习题集

一、解答题（共 7 题），解答过程应写出必要的文字说明、证明过程或演算步骤

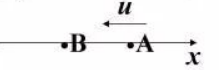
1. 已知一平面简谐波在介质中以波速

u = 10 m / s

沿

x

轴负方向传播, 已知波线上点

A

的振动方程为

y_{A} = 2 \cos (π t + π)

求：(1)以A点为坐标原点时的波函数
(2)以波线上与

A

相距

5 cm

的

B

点为坐标原点时的波函数

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

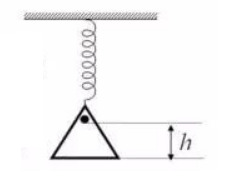
2. 劲度系数为

k

的轻弹簧下端挂一质量为

M

的静止盘。一质量为

m

的物体由距盘底

h

高处自由下落，与盘完全非弹性碰撞, 并与盘一起振动。以碰撞瞬间为计时起点, 系统平衡位置为坐标原点, 以坚直向下为

x

轴正向, 写出系统的振动方程。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 波长为

600 nm

的单色光垂直入射在一光栅上, 第2级明纹出现在

\sin φ_{2} = 0.20

处, 第 4 级缺级, 求: (1) 光栅常数

d;

; (2)光栅狭缝的最小宽度

a

; (3) 屏幕上实际可呈现的明纹级次。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 惯性系

S

中同一地点发生了两个事件, 事件 2 比事件 1 晚发生

Δ t = 2 s

; 而在惯性系

S^{'}

中, 观测事件 2 比事件 1 晚发生

Δ t^{'} = 3 s

. 那么在S'系中, 两事件发生的地点之间的距离是多少?

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 试用下列三种方法计算宽为

a

的无限深一维势阱中质量为

m

的粒子的最小能量: (1)德布罗意波的驻波条件; (2)不确定关系；(3)薛定谔方程。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

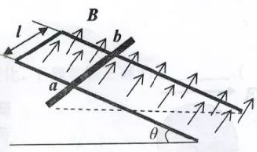
6. 无电阻的导体弯曲成

U

形导轨框架, 宽度为

l

, 与地面成

θ

角放置。开始时导体棒

a b

横向静止于导轨某处, 均匀磁场

B

垂直于导轨斜面指向斜上方, 如图所示. 设导轨足够长, 导体棒

a b

的质量为

m

, 与导轨之间的滑动摩擦系数为

μ

, 导体棒与导轨接触

l

长度的电阻恒为

r

. 重力加速度为

g

, 且

g \sin θ > μ g \cos θ

. 现将导体棒由静止释放并开始计时, 在滑动过程中与导轨始终保持良好接触, 不计接触电阻, 求其下滑速度

v

与时间

t

的关系式.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 有一缝宽为

0.1 mm

的单缝, 在其后侧放置一焦距为

1 m

的薄凸透镜。现用

λ = 480 nm

平行蓝光垂直照射该单缝, 求位于透镜像方焦平面处屏上第二级明纹的宽度 (注: 在衍射角很小时,

\sin θ \approx \tan θ \approx θ

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。