单选题 (共 15 题 ),每题只有一个选项正确
设集合 $M=\{x \mid 0 \leqslant x < 2\}$, 集合 $A=\left\{x \mid x^2-2 x-3 < 0\right\}$, 集合 $M \cap N=$
$\text{A.}$ $\{x \mid 0 \leq x < 1\}$
$\text{B.}$ $\{x \mid 0 \leq x < 2\}$
$\text{C.}$ $\{x \mid 0 \leq x \leq 1\}$
$\text{D.}$ $\{x \mid 0 \leq x \leq 2\}$
如果直线 $a x+2 y+2=0$ 与直线 $3 x-y-2=0$ 平行, 那么系数 $a=$
$\text{A.}$ -3
$\text{B.}$ -6
$\text{C.}$ $-\frac{3}{2}$
$\text{D.}$ $\frac{2}{3}$
函数 $y=\operatorname{tg}\left(\frac{1}{2} x-\frac{1}{2} \pi\right)$ 在一个周期内的图像是
$\text{A.}$ 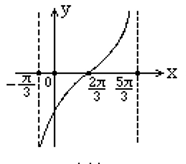 $\text{B.}$
$\text{B.}$ 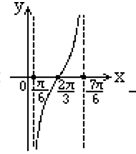 $\text{C.}$
$\text{C.}$ 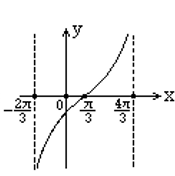 $\text{D.}$
$\text{D.}$ 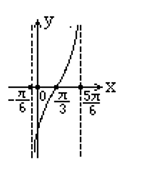
已知三棱锥 $D-A B C$ 的三个侧面与底面全等, 且 $A B=A C=\sqrt{3}, B C=2$, 则以 $B C$ 为棱, 以面 $B C D$ 与面 $B C A$ 为面的二面角的大小是
$\text{A.}$ $\arccos \frac{\sqrt{3}}{3}$
$\text{B.}$ $\arccos \frac{1}{3}$
$\text{C.}$ $\frac{\pi}{2}$
$\text{D.}$ $\frac{2 \pi}{3}$
函数 $y=\sin \left(\frac{\pi}{3}-2 x\right)+\cos 2 x$ 的最小正周期是
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\pi$
$\text{C.}$ $2 \pi$
$\text{D.}$ $4 \pi$
满足 $\arccos (1-x) \geq \arccos x$ 的 $x$ 的取值范围是
$\text{A.}$ $\left[-1,-\frac{1}{2}\right]$
$\text{B.}$ $\left[-\frac{1}{2}, 0\right]$
$\text{C.}$ $\left[0, \frac{1}{2}\right]$
$\text{D.}$ $\left[\frac{1}{2}, 1\right]$
将 $y=2^x$ 的图像 () 再作关于直线 $y=x$ 对称的图像, 可得到函数 $y=\log _2(x+1)$ 的图像.
$\text{A.}$ 先向左平行移动 1 个单位
$\text{B.}$ 先向右平行移动 1 个单位
$\text{C.}$ 先向上平行移动 1 个单位
$\text{D.}$ 先向下平行移动 1 个单位
长方体一个顶点上三条棱的长分别是 $3,4,5$, 且它的八个顶点都在同一个球面上, 这个球的表面积是
$\text{A.}$ $20 \sqrt{2} \pi$
$\text{B.}$ $25 \sqrt{2} \pi$
$\text{C.}$ $50 \pi$
$\text{D.}$ $200 \pi$
曲线的参数方程是 $\left\{\begin{array}{l}x=1-\frac{1}{t} \\ y=1-t^2\end{array}\right.$ ( $t$ 是参数, $\left.t \neq 0\right)$, 它的普通方程是
$\text{A.}$ $(x-1)^2(y-1)=1$
$\text{B.}$ $y=\frac{x(x-2)}{(1-x)^2}$
$\text{C.}$ $y=\frac{1}{(1-x)^2}-1$
$\text{D.}$ $y=\frac{x}{1-x^2}+1$
函数 $y=\cos ^2 x-3 \cos x+2$ 的最小值为
$\text{A.}$ 2
$\text{B.}$ 0
$\text{C.}$ $-\frac{1}{4}$
$\text{D.}$ 6
椭圆 $C$ 与椭圆 $\frac{(x-3)^2}{9}+\frac{(y-2)^2}{4}=1$ 关于直线 $x+y=0$ 对称, 椭圆 $C$ 的方程是
$\text{A.}$ $\frac{(x+2)^2}{4}+\frac{(y+3)^2}{9}=1$
$\text{B.}$ $\frac{(x-2)^2}{9}+\frac{(y-3)^2}{4}=1$
$\text{C.}$ $\frac{(x+2)^2}{9}+\frac{(y+3)^2}{4}=1$
$\text{D.}$ $\frac{(x-2)^2}{4}+\frac{(y-3)^2}{9}=1$
圆台上、下底面积分别为 $\pi 、 4 \pi$, 侧面积为 $6 \pi$, 这个圆台的体积是
$\text{A.}$ $\frac{2 \sqrt{3} \pi}{3}$
$\text{B.}$ $2 \sqrt{3} \pi$
$\text{C.}$ $\frac{7 \sqrt{3} \pi}{6}$
$\text{D.}$ $\frac{7 \sqrt{3} \pi}{3}$
定义在区间 $(-\infty,+\infty)$ 的奇函数 $f(x)$ 为增函数;偶函数 $g(x)$ 在区间 $[0,+\infty)$ 的图像与 $f(x)$ 的图像重合, 设 $a>b>0$, 给出下列不等式:
(1) $f(b)-f(-a)>g(a)-g(-b) ;$
(2) $f(b)-f(-a) < g(a)-g(-b) ; \mid$
(3) $f(a)-f(-b)>g(b)-g(-a)$;
(4) $f(a)-f(-b) < g(b)-g(-a)$,
其中成立的是
$\text{A.}$ (1)与(4)
$\text{B.}$ (2)与(3)
$\text{C.}$ (1)与(3)
$\text{D.}$ (2)与(4)
不等式组 $\left\{\begin{array}{l}x>0 \\ \frac{3-x}{3+x}>\left|\frac{2-x}{2+x}\right|\end{array}\right.$ 的解集是
$\text{A.}$ $\{x \mid 0 < x < 2\}$
$\text{B.}$ $\{x \mid 0 < x < 2.5\}$
$\text{C.}$ $\{x \mid 0 < x < \sqrt{6}\}$
$\text{D.}$ $\{x \mid 0 < x < 3\}$
四面体的顶点和各棱中点共 10 个点, 在其中取 4 个不共面的点, 不同的取法共有
$\text{A.}$ 150 种
$\text{B.}$ 147 种
$\text{C.}$ 144 种
$\text{D.}$ 141 种
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $\left(\frac{a}{x}-\sqrt{\frac{x}{2}}\right)^9$ 的展开式中 $x^3$ 的系数为 $\frac{9}{4}$, 常数 $a$ 的值为
已知直线的极坐标方程为 $\rho \sin \left(\theta+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}$, 则极点到该直线的距离是
$\frac{\sin 7^{\circ}+\cos 15^{\circ} \sin 8^{\circ}}{\cos 7^{\circ}-\sin 15^{\circ} \sin 8^{\circ}}$ 的值为
已知 $m, l$ 是直线, $\alpha 、 \beta$ 是平面, 给出下列命题:
(1)若 $l$ 垂直于 $\alpha$ 内的两条相交直线,则 $1 \perp \alpha$ ;
(2)若 $l$ 平行于 $\alpha$, 则 $l$ 平行于 $\alpha$ 内的所有直线;
(3)若 $m \subset \alpha, l \subset \beta$, 且 $l \perp m$, 则 $\alpha \perp \beta$;
(4)若 $l \subset \beta$, 且 $l \perp \alpha$, 则 $\alpha \perp \beta$;
(5)若 $m \subset \alpha, l \subset \beta$, 且 $\alpha / / \beta$, 则 $m / / l$.
其中正确的命题的序号是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知复数 $z=\frac{\sqrt{3}}{2}-\frac{1}{2} i, \omega=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i$. 复数 $\bar{z}, z^2 \omega^3$ 在复数平面上所对应的点分别为 $P, Q$. 证明 $\triangle O P Q$ 是等腰直角三角形 (其中 $O$ 为原点).
已知数列 $\left\{a_n\right\},\left\{b_n\right\}$ 都是由正数组成的等比数列, 公比分别为 $p 、 q$, 其中 $p>q$, 且 $p \neq 1$, $q \neq 1$. 设 $c_n=a_n+b_n, S_n$ 为数列 $\left\{c_n\right\}$ 的前 $n$ 项和. 求 $\lim _{n \rightarrow \infty} \frac{S_n}{S_{n-1}}$.
甲、乙两地相距 $S$ 千米, 汽车从甲地匀速行驶到乙地, 速度不得超过 $c$ 千米/时.知汽车每小时的运输成本 (以元为单位) 由可变部分和固定部分组成: 可变部分与速度 $V$ (千米/时) 的平方成正比、比例系数为 $b$ ;固定部分为 $a$ 元。
I. 把全程运输成本 $y$ (元) 表示为速度 $V$ (千米/时) 的函数, 并指出这个函数的定义域;
II. 为了使全程运输成本最小, 汽车应以多大速度行驶?
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $E 、 F$ 分别是 $B B_1$ 、 $C D$ 的中点.
I. 证明 $A L \perp D_1 F$;
II. 求 $A E$ 与 $D_1 F$ 所成的角;
III. 证明面 $A E L \perp$ 面 $A_1 F D_1$;
IV. 设 $A A_1=2$, 求三棱锥 $F-A_1 E D_1$ 的体积 $V_{F-A_1 E D_1}$

设二次函数 $f(x)=a x^2+b x+c(a>0)$, 方程 $f(x)-x=0$ 的两个根 $x_1, x_2$ 满足 $0 < x_1 < x_2 < \frac{1}{a}$.
I. 当 $x \in\left(0, x_1\right)$ 时, 证明 $x < f(x) < x_1$;
II. 设函数 $f(x)$ 的图像关于直线 $x=x_0$ 对称, 证明 $x_0 < \frac{x_1}{2} 25$.
设圆满足: (1) 截 $y$ 轴所得弦长为 2 ; (2)被 $x$ 轴分成两段圆弧, 其弧长的比为 $3: 1$, 在满足条件 (1)、(2)的所有圆中, 求圆心到直线 $1: x-2 y=0$ 的距离最小的圆的方程.