填空题 (共 8 题 ),请把答案直接填写在答题纸上
使得 $16000 \cdot\left(\frac{2}{5}\right)^n$ 的值是一个正整数的整数 $n$ 一共有个.
设动直线 $x=t$ 与函数 $y=f(x)$ 的图象交于点 $(t, f(t))$ ,与函数 $y=g(x)$ 的图象交于点 $Q(t, g(t))$ ,当 $a \leqslant t \leqslant b$ 时,总有 $P Q \leqslant 1$ 恒成立,则称函数 $f(x)$ 与 $g(x)$ 在 $a \leqslant x \leqslant b$ 上是 “逼近函数”. 则下列结论:
①函数 $y=-\frac{x}{2}$ 与 $y=\frac{x}{2}$ 在 $-1 \leqslant x \leqslant 1$ 上是 “逼近函数”;
② 函数 $y=5 x$ 与 $y=x^2+5$ 在 $3 \leqslant x \leqslant 4$ 上是 “逼近函数”;
③ 函数 $y=x^2-1$ 与 $y=2 x^2-x$ 在 $0 \leqslant x \leqslant 1$ 是 “逼近函数”.
其中,正确的是
如果方程 $x^3-7 x^2+(10+k) x-2 k=0$ 的三个根可以作为一个等腰三角形的三边长,则实数 $k=$
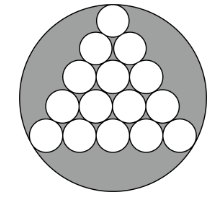
如图,一个较大的圆内有 15 个半径为 1 的小圆,所有的交点都为切点,图中阴影为大圆内但在所有小圆外部分,则阴影部分的面积为
如图,在平面直角坐标系上, $A(-6,0) , B(-2,2)$ ,动点 $P$ 在直线 $y=-x$ 上,动点 $Q$ 在 $x$ 轴上,则 $A P+P Q+Q B$ 的最小值为

如图,一只小虫沿着图示的由六边形构成的格子从点 $A$ 爬行到点 $B$ ,标记有箭头的边只能按箭头方向爬行,且小虫爬行同一条边最多一次,则共有 ( ) 种不同的爬行路径.

如图是一个正方体的表面展开图,将展开图折甾成正方体后,相对面上两个数之和为 5 ,则 $\mathrm{x}+\mathrm{y}=$

如图1,在平面直角坐标系中,抛物线 $y=-\frac{1}{2} x^2-x+4$ 与 $x$ 轴分别交于 $A, B$ 两点 (点 $A$ 在点 $B$ 左侧),与 $y$ 轴交于 $C$ 点.
(1)求 $\triangle A B C$ 的面积;
(2)点 $P$ 为直线 $A C$ 上方抛物线上的任意一点,过点 $P$ 作 $P D \| y$ 轴交直线 $A C$ 于点 $D$ ,求 $P D+\frac{\sqrt{2}}{2} C D$ 的最大值及此时点 $P$ 的坐标; (3)如图 2 ,将抛物线沿着水平方向向右平移 2 个单位长度得到新的抛物线,点 $E$ 为原抛物线与平移后的抛物线的交点,点 $M$ 为平移后的抛物线对称轴上的一动点,点 $N$ 为坐标平面内的一点,直接写出所有使得以点 $B 、 E 、 M 、 N$ 为顶点的四边形是菱形的点 $\mathrm{N}$ 的坐标,并把求其中一个点 $N$ 的坐标的求解过程写出来.

解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
有一矩形纸片 $A B C D , A B=a , A D=b$ ,将矩形 $A B C D$ 沿对角线 $A C$ 对折后放于桌面上,探究其覆盖桌面的面积.

我们学习了实数与向量相乘,对于两个非零向量 $\vec{a}$ 和 $\vec{b}$ 且 $\vec{a} / / \vec{b}$ 存在唯一的实数 $\lambda$ ,使得 $\vec{a}=\lambda \vec{b}$ ,记作 $f(\vec{a}, \vec{b})=\lambda$. 如图,已知 $A , B , C$ , $D$ 为同一直线上顺次四点.
(1) 若 $f(\overrightarrow{A D}, \overrightarrow{D B})=-2$, 则 $f(\overrightarrow{D B}, \overrightarrow{A D})=$.
(2) 若 $\frac{f(\overrightarrow{A C}, \overrightarrow{C B})}{f(\overrightarrow{A D}, \overrightarrow{D B})}=-1$ ,则称 $A, B , C , D$ 为调和点列,请探究此时 $A B , A C, A D$ 这三条线段的长度满足的关系式,并证明.
