单选题 (共 13 题 ),每题只有一个选项正确
.一均匀带电球面,电荷面密度为 $\sigma$, 球面内电场强度处处为零, 球面上面元 $\mathrm{d} S$ 带有 $\mathcal{} \sigma \mathrm{d} S$ 的电荷, 该电荷在球面内各 点产生的电场强度
$\text{A.}$ 处处为零
$\text{B.}$ 不一定都为零
$\text{C.}$ 处处不为零
$\text{D.}$ 无法判定
设有一“无限大”均匀带正电荷的平面. 取 $x$ 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度 $\vec{E}$ 随距离平面的位置坐标 $x$ 变化的关系曲线为(规定场强方向沿 $x$ 轴正向为正、反之为负):
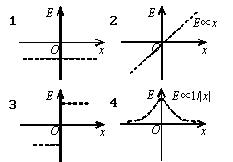
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
有一边长为 $a$ 的正方形平面,在其中垂线上距中心 $O_{\text {点 }}{ }^{a / 2}$ 处,有一电荷为 $q$ 的正点电荷,如图所示,则通过该平面的 电场强度通量为
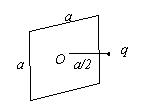
$\text{A.}$ $\frac{q}{3 \varepsilon_0}$
$\text{B.}$ $\frac{q}{4 \pi \varepsilon_0}$
$\text{C.}$ $\frac{q}{3 \pi \varepsilon_0}$
$\text{D.}$ $\frac{q}{6 \varepsilon_0}$
半径为 $R$ 的均匀带电球面的静电场中各点的电场强度的大小 $E$ 与距球心的距离 $r$ 之间的关系曲线为:

$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
半径为 $R$ 的均匀带电球体的静电场中各点的电场强度的大小 $E$ 与距球心的距离 $r$ 的关系曲线为

$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
两个同心均匀带电球面,半径分别为 $R_a$ 和 $R_b\left(R_a < R_b\right)$, 所带电荷分别为 $Q_a$ 和 $Q_b$. 设某点与球心相距 $r$, 当 $R_a < r < R_b$ 时, 该点的电场强度的大小为
$\text{A.}$ $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q_a+Q_b}{r^2}$
$\text{B.}$ $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q_a-Q_b}{r^2}$
$\text{C.}$ $\frac{1}{4 \pi \varepsilon_0} \cdot\left(\frac{Q_a}{r^2}+\frac{Q_b}{R_b^2}\right)$
$\text{D.}$ $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q_a}{r^2}$
高斯定理 $\oint_S \vec{E} \cdot \mathrm{d} \vec{S}=\int_V \rho \mathrm{d} V / \varepsilon_0$
$\text{A.}$ 适用于任何静电场.
$\text{B.}$ 只适用于真空中的静电场.
$\text{C.}$ 只适用于具有球对称性、轴对称性和平面对称性的静电场。
$\text{D.}$ 只适用于虽然不具有 C 中所述的对称性、但可以找到合适的高斯面的静电场 .
在点电荷 $+q$ 的电场中,若取图中 $P$ 点处为电势零点,则 $M$ 点的电势为
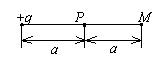
$\text{A.}$ $\frac{q}{4 \pi \varepsilon_0 a}$
$\text{B.}$ $\frac{q}{8 \pi \varepsilon_0 a}$
$\text{C.}$ $\frac{-q}{4 \pi \varepsilon_0 a}$
$\text{D.}$ $\frac{-q}{8 \pi \varepsilon_0 a}$
如图,在点电荷 $q$ 的电场中,选取以 $q$ 为中心、 $R$ 为半径的球面上一点 $P$ 处作电势零点, 则与点电荷 $q$ 距离为 $r$ 的 $P^r$ 点的电势为
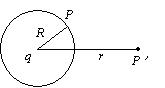
$\text{A.}$ $\frac{q}{4 \pi \varepsilon_0 r}$
$\text{B.}$ $\frac{q}{4 \pi \varepsilon_0}\left(\frac{1}{r}-\frac{1}{R}\right)$
$\text{C.}$ $\frac{q}{4 \pi \varepsilon_0(r-R)}$
$\text{D.}$ $\frac{q}{4 \pi \varepsilon_0}\left(\frac{1}{R}-\frac{1}{r}\right)$
如图所示, 半径为 $R$ 的均匀带电球面, 总电荷为 $Q$, 设无穷远处的电势为零, 则球内距离球心为 $r$ 的 $P$ 点处的电场强 度的大小和电势为
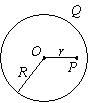
$\text{A.}$ $E=0, U=\frac{Q}{4 \pi \varepsilon_0 r}$
$\text{B.}$ $E=0 \quad U=\frac{Q}{4 \pi \varepsilon_0 R}$
$\text{C.}$ $E=\frac{Q}{4 \pi \varepsilon_0 r^2} \quad U=\frac{Q}{4 \pi \varepsilon_0 r}$
$\text{D.}$ $E=\frac{Q}{4 \pi \varepsilon_0 r^2} \quad U=\frac{Q}{4 \pi \varepsilon_0 R}$
在边长为 $a$ 的正方体中心处放置一点电荷 $Q$, 设无穷远处为电势零点, 则在正方体顶角处的电势为:
$\text{A.}$ $\frac{Q}{4 \sqrt{3} \pi \varepsilon_0 a}$
$\text{B.}$ $\frac{Q}{2 \sqrt{3} \pi \varepsilon_0 a}$
$\text{C.}$ $\frac{Q}{6 \pi \varepsilon_0 a}$
$\text{D.}$ $\frac{Q}{12 \pi \varepsilon_0 a}$
如图所示, 两个同心的均匀带电球面, 内球面半径为 $R_1$ 、带电荷 $Q_1$, 外球面半径为 $R_2$ 、带电荷 $Q_2$. 设无穷远处为电势 零点,则在两个球面之间、距离球心为 $r$ 处的 $P$ 点的电势 $U$ 为
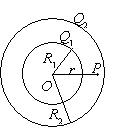
$\text{A.}$ $\frac{Q_1+Q_2}{4 \pi \varepsilon_0 r}$
$\text{B.}$ $\frac{Q_1}{4 \pi \varepsilon_0 R_1}+\frac{Q_2}{4 \pi \varepsilon_0 R_2}$
$\text{C.}$ $\frac{Q_1}{4 \pi \varepsilon_0 r}+\frac{Q_2}{4 \pi \varepsilon_0 R_2}$
$\text{D.}$ $\frac{Q_1}{4 \pi \varepsilon_0 R_1}+\frac{Q_2}{4 \pi \varepsilon_0 r}$
点电荷 $-q$ 位于圆心 $O$ 处, $A 、 B 、 C 、 D$ 为同一圆周上的四点, 如图所示. 现将一试验电荷从 $A$ 点分别移动到 $B 、$ $C 、 D$ 各点, 则
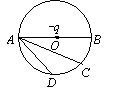
$\text{A.}$ 从 $A$ 到 $B$ ,电场力作功最大
$\text{B.}$ 从 $A$ 到 $C$, 电场力作功最大
$\text{C.}$ 从 $A$ 到 $D$ ,电场力作功最大
$\text{D.}$ 从 $A$ 到各点, 电场力作功相等
填空题 (共 1 题 ),请把答案直接填写在答题纸上
如图所示, 真空中一长为 $L$ 的均匀带电细直杆, 总电荷为 $q$, 试求在直杆延长线上距杆的一端距离为 $d$ 的 $\mathrm{P}$ 点的电场强度。

解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
电荷 $q$ 均匀分布在长为 $2 l$ 的细杆上, 求在杆外延长线上与杆端距离为 $a$ 的 $P$ 点的电势 (设无穷远处为电势零点)
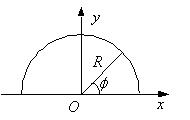
带电细线弯成半径为 $R$ 的半圆形, 电荷线密度为 $\lambda=\lambda_0 \sin \varphi$, 式中 ${\lambda_0}$ 为一常数, $\phi$为半径 $ R$ 与 $x$ 轴所成的夹角, 如图所示, 试求环心 $O$ 处的电场强度.
在强度的大小为 $E$, 方向坚直向上的匀强电场中, 有一半径为 $R$ 的半球形光滑绝缘槽放在光滑水平面上(如图所示 ) 槽的质量为 $M$, 一质量为 $m$ 带有电荷 ${+q}$ 的小球从槽的顶点 $A$ 处由静止释放. 如果忽略空气阻力且质点受到的重 力大于其所受电场力, 求:
(1)小球由顶点 $A$ 滑至半球最低点 $B$ 时相对地面的速度;
(2)小球通过 $B$ 点时,槽相对地面的速度;
(3)小球通过 $B$ 点后,能不能再上升到右端最高点 $C$ ?

实验表明, 在靠近地面处有相当强的电场, 电场强度 $\vec{E}$ 垂直于地面向下, 大小约为 $100 \mathrm{~N} / \mathrm{C}$; 在离地面 $1.5 \mathrm{~km}$ 高的地 $\vec{E}$ 也是垂直向下的,大约为 $23N/C$
(1)假设地面上各处 $\vec{E}$都是垂直向下,试计划从地面到此高度大气中电荷的平均密度
(2)假设地表面内电场强度为零,且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生,求地面上的电荷面密度.已知:真空介电常量 $\left[\varepsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 / \mathrm{N}^2 \mathrm{~m}^2\right]$