单选题 (共 8 题 ),每题只有一个选项正确
节约水 5 吨记作 +5 吨,则浪费水 2 吨记作
$\text{A.}$ -3 吨
$\text{B.}$ +2 吨
$\text{C.}$ -2 吨
$\text{D.}$ +3 吨
如图为出现在深圳街头的新型无线充电石墩,关于石墩的三视图的描述,正确的是

$\text{A.}$ 主视图和左视图相同
$\text{B.}$ 主视图和俯视图相同
$\text{C.}$ 左视图和俯视图相同
$\text{D.}$ 三个视图都相同
某校进行《九章算术》,《周髀算经》,《孙子算经》,《算法统宗》四本书的长文本阅读活动,小聪从中任取一本,恰好抽到《九章算术》的概率为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{2}{3}$
如图为人行天桥的示意图,若高 $B C$ 长为 10 米,斜道 $A C$ 长为 30 米,则 $\sin A$ 的值为
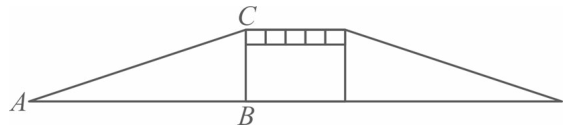
$\text{A.}$ $\frac{2 \sqrt{2}}{3}$
$\text{B.}$ 3
$\text{C.}$ $\frac{\sqrt{2}}{4}$
$\text{D.}$ $\frac{1}{3}$
下列计算正确的是
$\text{A.}$ $a^2+a^4=a^6$
$\text{B.}$ $a^3 \cdot a^3=a^6$
$\text{C.}$ $\left(a^2\right)^3=a^5$
$\text{D.}$ $(a+b)^2=a^2+b^2$
如图为小颖在试鞋镜前的光路图,入射光线 $O A$ 经平面镜后反射入眼,若 $C B / / O A, \angle C B O=122^{\circ}$ , $\angle B O N=90^{\circ}$ ,则入射角 $\angle A O N$ 的度数为
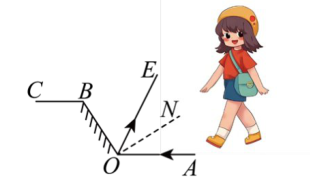
$\text{A.}$ $22^{\circ}$
$\text{B.}$ $32^{\circ}$
$\text{C.}$ $35^{\circ}$
$\text{D.}$ $122^{\circ}$
某社区植树 60 棵,实际种植人数是原计划人数的 2 倍,实际平均每人种植棵树比原计划少了 3 棵.若设 原计划人数为 $x$ 人,则下列方程正确的是( )
$\text{A.}$ $\frac{60}{x}-\frac{60}{2 x}=3$
$\text{B.}$ $\frac{60}{2 x}-\frac{60}{x}=3$
$\text{C.}$ $\frac{60}{x}=2 \times \frac{60}{x+3}$
$\text{D.}$ $\frac{60}{x}=2 \times \frac{60}{x-3}$
如图,将正方形 $A B C D$ 沿 $E F$ 折叠,使得点 A 与对角线的交点 $O$ 重合,$E F$ 为折痕,则 $\frac{E F}{C G}$ 的值为( )
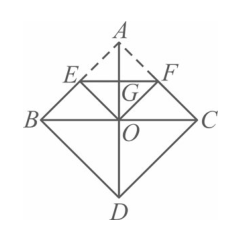
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $\frac{2}{3}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
若关于 $x$ 的方程 $x+a=5$ 的解为 $x=1$ ,则 $a=$
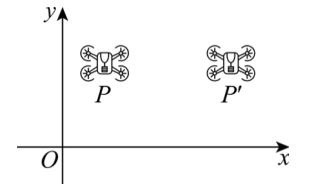
如图,将无人机沿着 $x$ 轴向右平移 3 个单位,若无人机上一点 $P$ 的坐标为 $(1,2)$ ,则平移后点 $P$ 的坐标为
计算:$\frac{a^2}{a+1}-\frac{1}{a+1}=$
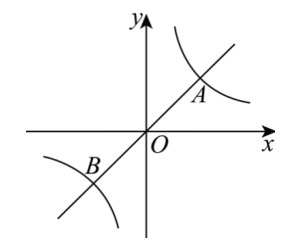
如图,同一平面直角坐标系下的正比例函数 $y=a x$ 与反比例函数 $y=\frac{2-a}{x}$ 相交于点 A 和点 $B$ .若 A 的横坐标为 1 ,则 $B$ 的坐标为
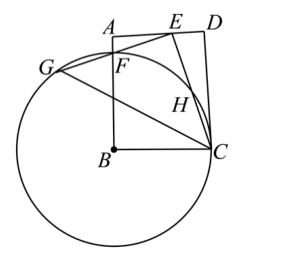
如图,以矩形 $A B C D$ 的 $B$ 点为圆心,$B C$ 的长为半径作 $\odot B$ ,交 $A B$ 于点 $F$ ,点 $E$ 为 $A D$ 上一点,连接 $C E$ ,将线段 $C E$ 绕点 $E$ 顺时针旋转至 $E G$ ,点 $G$ 落在 $\odot B$ 上,且点 $F$ 为 $E G$ 中点.若 $A F=1$ , $A E=3$ ,则 $C D$ 的长为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:$\sqrt{16}+|-3|+(\pi-3.14)^0+(-1)^{2025}$ .
解一元一次方程组 $\left\{\begin{array}{l}2 x \geq x-1 ...(1) \\ \frac{1}{2}(x+2) < 3 ...(2)\end{array}\right.$ ,并在数轴上表示.
解:由不等式(1)得: $\_\_\_\_$ ,
由不等式(2)得: $\_\_\_\_$ ,
在数轴上表示为:
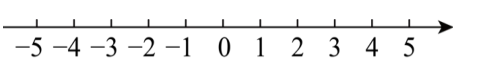
所以,原不等式组的解集为
某班级拟开展科技主题班会活动,现从"科技安全","科技畅想","科技生活","科技前沿","科技故事"中挑选一个主题。全班同学通过投票选出最受欢迎的主题,投票结果的条形统计图与扇形统计图如下:
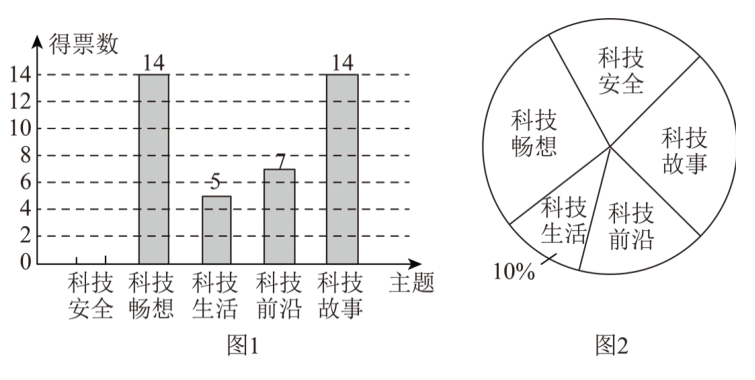
请根据以上信息,完成下列问题:
(1)本次投票共 $\_\_\_\_$人参与,其中科技安全所占百分比为 $\_\_\_\_$ ,并补全条形统计图。
(2)为确定班会科技主题,从该班选择7名学生代表为"科技畅想"和"科技故事"打分,分数列表如下:
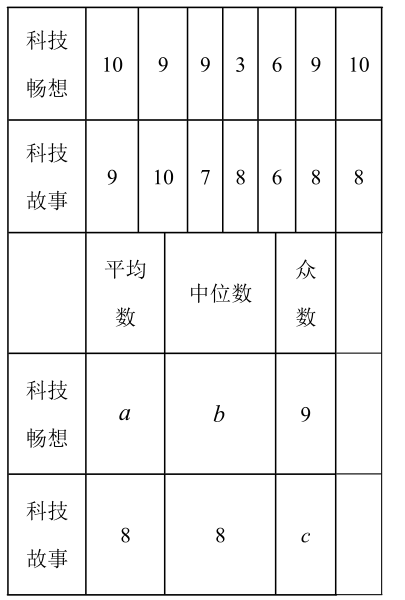
求表中的数据:$a=$ $\_\_\_\_$ ,$b=$ $\_\_\_\_$ ,$c=$ $\_\_\_\_$
(3)结合上述信息,应该选择哪个科技主题,并说明理由.
某学校采购体育用品,需要购买三种球类.已知某体育用品商店排球的单价为 30 元/个,篮球,足球的价格如下表:
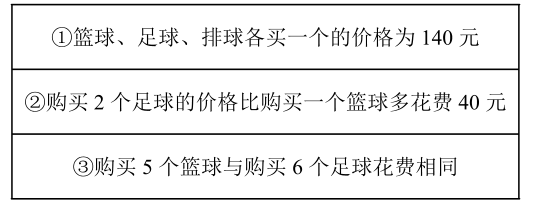
(1)请你从上述 3 个条件中任选 2 个作为条件,求出篮球和足球的单价;
(2)若该学校要购买篮球,足球共 10 个,且足球的个数不超过篮球个数的 2 倍,请问购买多少个篮球时,花费最少,最少费用是多少?
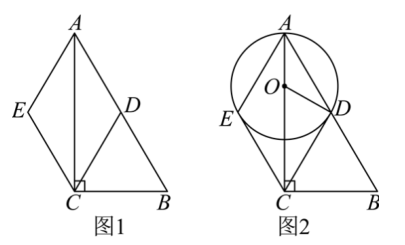
如图 1,在 Rt $\triangle A B C$ 中,$D$ 是 $A B$ 的中点,$A E=C D, A D=E C$ .
(1)求证:四边形 $A D C E$ 为菱形;
(2)如图 2,若点 $O$ 为 $A C$ 上一点,且 $E, \mathrm{~A}, D$ 三点均在 $\odot O$ 上,连接 $O D, C D$ 与 $\odot O$ 相切于点 D ,
① 求 $\angle A C D=$ $\_\_\_\_$ ;
② 求 $\odot O$ 的半径 $r$ ;
(3)利用圆规和无刻度直尺在图 2 中作射线 $D F / / A C$ ,交 $B C$ 于点 $D$ ,保留作图痕迹,不用写出作法和理由.
综合与实践
【问题背景】排队是生活中常见的场景,如图,某数学小组针对某次演出,研究了排队人数与安检时间,安排通道数之间的关系.
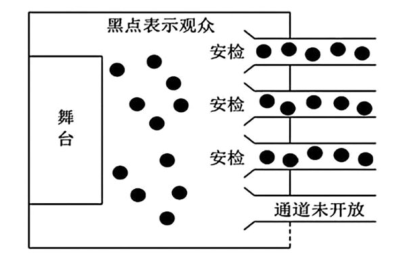
【研究条件】
条件 1:观众进场立即排队安检,在任意时刻都满足:排队人数=现场总人数-已入场人数;
条件 2:若该演出场地最多可开放 9 条安检通道,平均每条通道每分钟可安检 6 人.
【模型构建】若该演出前 30 分钟开始进行安检,经研究发现,现场总人数 $y$ 与安检时间 $x$ 之间满足关系式: $y=-x^2+60 x+100(0 \leq x \leq 30)$
结合上述信息,请完成下述问题:
(1)当开通 3 条安检通道时,安检时间 $x$ 分钟时,已入场人数为 $\_\_\_\_$ ,排队人数 $w$ 与安检时间 $x$ 的函数关系式为 $\_\_\_\_$ .
【模型应用】
(2)在(1)的条件下,排队人数在第几分钟达到最大值,最大人数为多少?
(3)已知该演出主办方要求:
① 排队人数在安检开始 10 分钟内(包含 10 分钟)减少;
② 尽量少安排安检通道,以节省开支.
若同时满足以上两个要求,可开设几条安检通道,请说明理由?
【总结反思】
函数可刻画生活实际场景,但要注意验证模型的正确性,未来可结合更多变量(如突发情况、安检流程优化等)进行更深入的分析,以提高模型的准确性和实用性.
综合与探究
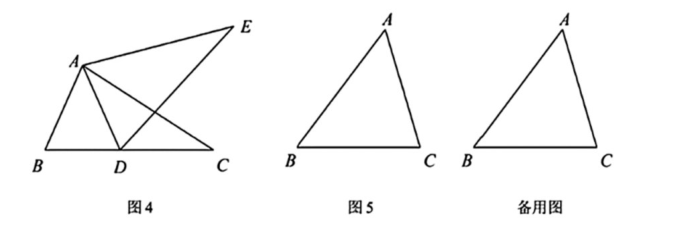
【探索发现】如图 1,小军用两个大小不同的等腰直角三角板拼接成一个四边形.
【抽象定义】以等腰三角形为边向外作等腰三角形,使该边所对的角等于原等腰三角形的顶角,此时该四边形称为"双等四边形",原等腰三角形称为四边形的"伴随三角形".如图 2,在 $\triangle A B C$ 中,$A B=A C$ , $A C=A D, \angle D=\angle B A C$ .此时,四边形 $A B C D$ 是"双等四边形", $ \triangle A B C$ 是"伴随三角形".
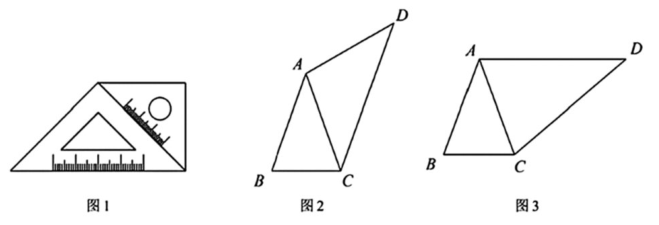
【问题解决】如图 3,在四边形 $A B C D$ 中,$A B=A C, A D=C D, \angle D=\angle B A C$ .求:
① $A D$ 与 $B C$ 的位置关系为: $\_\_\_\_$ :
② $A C^2$ $\_\_\_\_$ $A D \cdot B C$. (填">","<"或"=")
【方法应用】 ① 如图4,将 $\mathrm{V} A B C$ 绕点 A 逆时针旋转至 $\mathrm{V} A D E$ ,点 $D$ 恰好落在 $B C$ 边上,求证:四边形 $A B D E$ 是双等四边形.
② 如图 5,在等腰三角形 $A B C$ 中,$A C=B C, \cos B=\frac{3}{5}, A B=5$ ,在平面内找一点 $D$ ,使四边形 $A B C D$是以 $\triangle A B C$ 为伴随三角形的双等四边形,若存在,请求出 $C D$ 的长,若不存在,请说明理由.