综合与实践
【问题背景】排队是生活中常见的场景，如图，某数学小组针对某次演出，研究了排队人数与安检时间，安排通道数之间的关系．



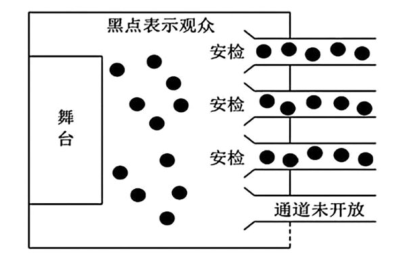
【研究条件】

条件 1：观众进场立即排队安检，在任意时刻都满足：排队人数＝现场总人数－已入场人数；
条件 2：若该演出场地最多可开放 9 条安检通道，平均每条通道每分钟可安检 6 人．
【模型构建】若该演出前 30 分钟开始进行安检，经研究发现，现场总人数 $y$ 与安检时间 $x$ 之间满足关系式： $y=-x^2+60 x+100(0 \leq x \leq 30)$

结合上述信息，请完成下述问题：
（1）当开通 3 条安检通道时，安检时间 $x$ 分钟时，已入场人数为 $\_\_\_\_$ ，排队人数 $w$ 与安检时间 $x$ 的函数关系式为 $\_\_\_\_$ ．

【模型应用】
（2）在（1）的条件下，排队人数在第几分钟达到最大值，最大人数为多少？
（3）已知该演出主办方要求：
① 排队人数在安检开始 10 分钟内（包含 10 分钟）减少；
② 尽量少安排安检通道，以节省开支．
若同时满足以上两个要求，可开设几条安检通道，请说明理由？
【总结反思】
函数可刻画生活实际场景，但要注意验证模型的正确性，未来可结合更多变量（如突发情况、安检流程优化等）进行更深入的分析，以提高模型的准确性和实用性．