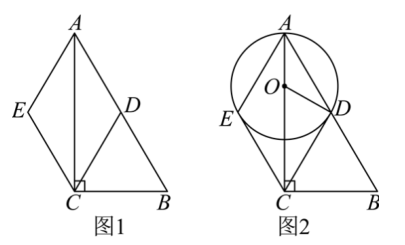
如图 1，在 Rt $\triangle A B C$ 中，$D$ 是 $A B$ 的中点，$A E=C D, A D=E C$ ．
（1）求证：四边形 $A D C E$ 为菱形；
（2）如图 2，若点 $O$ 为 $A C$ 上一点，且 $E, \mathrm{~A}, D$ 三点均在 $\odot O$ 上，连接 $O D, C D$ 与 $\odot O$ 相切于点 D ，
① 求 $\angle A C D=$ $\_\_\_\_$ ；
② 求 $\odot O$ 的半径 $r$ ；
（3）利用圆规和无刻度直尺在图 2 中作射线 $D F / / A C$ ，交 $B C$ 于点 $D$ ，保留作图痕迹，不用写出作法和理由．