数学活动:探究平面图形的最小覆盖圆
【定义】我们称能完全覆盖某平面图形的圆(即该平面图形上所有的点均在圆内或圆上)为该平面图形的覆盖圆.其中,能完全覆盖平面图形的最小的圆(即直径最小)称为该平面图形的最小覆盖圆.
【探究一】线段的最小覆盖圆
线段 $A B$ 的覆盖圆有无数个,其中,以 $A B$ 为直径的圆是其最小覆盖圆.
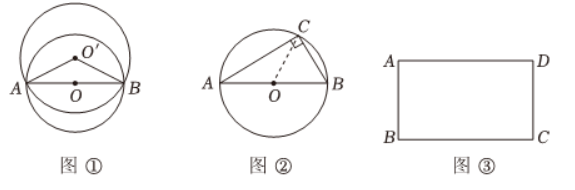
理由如下:易知线段 $A B$ 的最小覆盖圆一定经过点 $A$ 、点 $B$ 。如图(1),以 $A B$ 为直径作 $\odot O$ ,再过 $A$ 、 $B$ 两点作 $\odot O^{\prime}$( $O^{\prime}$ 与 $O$ 不重合),连结 $O^{\prime} A, O^{\prime} B$ 。
在 $\triangle O^{\prime} A B$ 中,有 $O^{\prime} A+O^{\prime} B>A B(\mathbf{\Delta})$ .
$$
\because O^{\prime} A=O^{\prime} B,
$$
$\therefore 2 O^{\prime} A>A B$ ,即 $\odot O^{\prime}$ 的直径大于 $\odot O$ 的直径.
$\therefore \odot O$ 是线段 $A B$ 的最小覆盖圆.
" $\mathbf{\Delta}$"处应填写的推理依据为 $\_\_\_\_$ .
【探究二】直角三角形的最小覆盖圆
要确定直角三角形的最小覆盖圆,我们可先将其转化为【探究一】中线段的最小覆盖圆问题.这样就可以先确定直角三角形最长边(斜边)的最小覆盖圆,再判断直角顶点与这个圆的位置关系,从而确定直角三角形的最小覆盖圆.
如图(2),在Rt $\triangle A B C$ 中,$\angle A C B=90^{\circ} . \odot O$ 是以 $A B$ 为直径的圆.
请你判断点 $C$ 与 $\odot O$ 的位置关系,并说明理由.
又由【探究一】可知,$\odot O$ 是Rt $\triangle A B C$ 最长边 $A B$ 的最小覆盖圆,所以,$\odot O$ 是Rt $\triangle A B C$ 的最小覆盖圆.
【拓展应用】矩形的最小覆盖圆
如图(3),在矩形 $A B C D$ 中,$A B=1 \mathrm{~cm}, B C=2 \mathrm{~cm}$ .
(1)用圆规和无刻度的直尺在图(3)中作矩形 $A B C D$ 的最小覆盖圆;
(不写作法,保留作图痕迹,作图确定后必须用黑色字迹的签字笔描黑)
(2)该矩形 $A B C D$ 的最小覆盖圆的直径为 $\_\_\_\_$ cm;
(3)若用两个等圆完全覆盖矩形 $A B C D$ ,则这样的两个等圆的最小直径为 $\_\_\_\_$ cm .