单选题 (共 4 题 ),每题只有一个选项正确
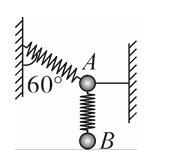
如图所示,一根弹簧一端固定在左侧坚直墙上,另一端连着 $A$ 小球,同时水平细线一端连着 $A$ 球,另一端固定在右侧坚直墙上,弹簧与坚直方向的夹角是 $60^{\circ}, A 、 B$两小球分别连在另一根坚直弹簧两端。开始时 $A 、 B$ 两球都静止不
动,$A 、 B$ 两小球的质量相等,重力加速度为 $g$ ,若不计弹簧质量,在水平细线被剪断瞬间,$A 、 B$ 两球的加速度分别为
$\text{A.}$ $a_A=a_B=g$
$\text{B.}$ $a_A=2 g, a_B=0$
$\text{C.}$ $a_A=\sqrt{3} g, a_B=0$
$\text{D.}$ $a_A=2 \sqrt{3} g, a_B=0$
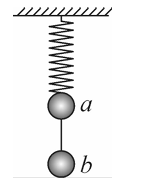
如图所示,两小球悬挂在天花板上, $a 、 b$ 两小球用细线连接,上面是一根轻质弹簧,$a 、 b$ 两球的质量分别为 $m$和 $2 m$ ,在细线烧断瞬间,$a 、 b$ 两球的加速度分别为 $a_1 、 a_2$ ,则:(取向下为正方向,重力加速度为 $g$ )
$\text{A.}$ $a_1=0, a_2=g$
$\text{B.}$ $a_1=g, a_2=g$
$\text{C.}$ $a_1=-2 g, a_2=g$
$\text{D.}$ $a_1=-g, a_2=0$
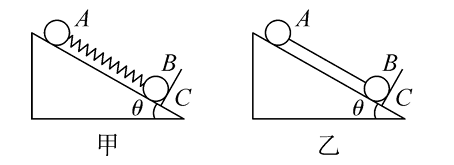
如图,$A 、 B$ 两球质量相等,光滑斜面的倾角为 $\theta$ ,图甲中,$A 、 B$ 两球用轻弹簧相连,图乙中 $A 、 B$ 两球用轻质杆相连,系统静止时,挡板 $C$与斜面垂直,弹簧、轻杆均与斜面平行,则在突然撤去挡板的瞬间
$\text{A.}$ 图甲中 $A$ 球的加速度不为零
$\text{B.}$ 图乙中两球加速度均为 $g \sin \theta$
$\text{C.}$ 图乙中轻杆的作用力一定不为零
$\text{D.}$ 图甲中 $B$ 球的加速度是图乙中 $B$ 球加速度的 3 倍
一质量为 $m$ 的乘客乘坐坚直电梯下楼,其位移 $s$ 与时间 $t$ 的关系图像如图所示。其中 $t_1 \sim t_2$ 段 $s-t$ 图像是直线,乘客所受支持力的大小用 $F_N$ 表示,速度大小用 $v$ 表示。重力加速度大小为 $g$ 。以下判断正确的是
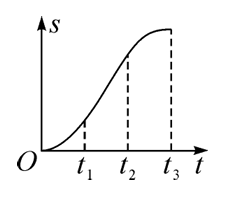
$\text{A.}$ $0 \sim t_1$ 时间内,$v$ 增大,$F_N>m g$
$\text{B.}$ $t_1 \sim t_2$ 时间内,$v$ 减小,$F_N < m g$
$\text{C.}$ $t_2 \sim t_3$ 时间内,$v$ 增大,$F_N < m g$
$\text{D.}$ $t_2 \sim t_3$ 时间内,$v$ 减小,$F_N> m g$
多选题 (共 8 题 ),每题有多个选项正确
如图所示,质量均为 $m$ 的木块 $A$ 和 $B$ 用一轻弹簧相连,坚直放在光滑的水平面上,木块 $A$上放有质量为 $2 m$ 的木块 $C$ ,三者均处于静止状态。现将木块 $C$ 迅速移开,若重力加速度为 $g$ ,则在木块 $C$ 移开的瞬间
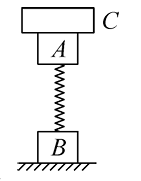
$\text{A.}$ 弹簧的形变量不改变
$\text{B.}$ 弹簧的弹力大小为 $m g$
$\text{C.}$ 木块 $A$ 的加凁度大小为 $2 g$
$\text{D.}$ 木块 $B$ 对水平面的压力大小迅速变为 $2 m g$
如图所示,质量为 $m$ 的小球被一根橡皮筋 $A C$和一根绳 $B C$ 系住,当小球静止时,橡皮筋处在水平方向上。下列判断中正确的是
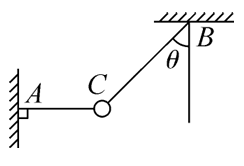
$\text{A.}$ 在 $A C$ 被突然剪断的瞬间,$B C$ 对小球的拉力不变
$\text{B.}$ 在 $A C$ 被突然剪断的瞬间,小球的加速度大小为 $g \sin \theta$
$\text{C.}$ 在 $B C$ 被突然剪断的瞬间,小球的加速度 大小为 $ \frac{g}{\cos \theta}$
$\text{D.}$ 在 $B C$ 被突然剪断的瞬间,小球的加速度大小为 $g \sin \theta$
如图甲所示,轻弹簧坚直固定在水平面上,一质量为 $m=0.2 \mathrm{~kg}$ 的小球,从弹簧上端某高度处自由下落,从它接触弹簧到弹簧压缩至最短的过程中(弹簧始终在弹性限度内),其速度 $v$ 和弹簧压缩量 $\Delta x$ 之间的函数图像如图乙所示,其中 $A$ 为曲线的最高点,小球和弹簧接触瞬间机械能损失不计,$g=10 \mathrm{~m} / \mathrm{s}^2$ ,则下列说法正确的是
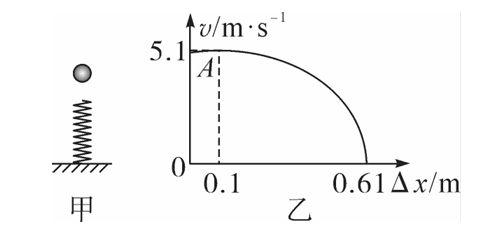
$\text{A.}$ 小球刚接触弹簧时速度最大
$\text{B.}$ 当 $\Delta x=0.3 \mathrm{~m}$ 时,小球处于超重状态
$\text{C.}$ 该弹簧的劲度系数为 $20.0 \mathrm{~N} / \mathrm{m}$
$\text{D.}$ 从接触弹簧到压缩至最短的过程中,小球的加速度先减小后增大
蹦床属于体操运动的一种,有"空中芭蕾"之称。某次比赛过程中,一运动员做蹦床运动时,利用力传感器测得运动员所受蹦床弹力 $F$ 随时间 $t$ 的变化图像如图所示。若运动员仅在坚直方向运动,不计空气阻力,取重力加速度大小 $g=10 \mathrm{~m} / \mathrm{s}^2$ ,依据图像给出的信息,下列说法正确的是
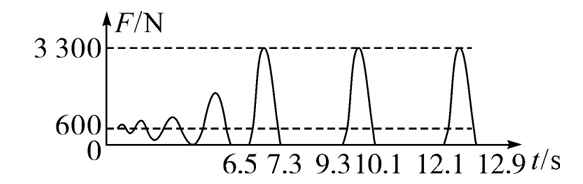
$\text{A.}$ 运动员的质量为 60 kg
$\text{B.}$ 运动员的最大加速度为 $45 \mathrm{~m} / \mathrm{s}^2$
$\text{C.}$ 运动员离开蹦床后上升的最大高度为 5 m
$\text{D.}$ 9.3 s 至 10.1 s 内,运动员一直处于超重
2021年9月17日,"神舟十二号"返回舱成功返回,返回舱在距地面某一高度时,启动减速降落伞开始做减速运动。当返回舱的速度大约减小至 $v=9 \mathrm{~m} / \mathrm{s}$ 时,继续匀速(近似)下降。当以这个速度一直降落到距离地面 $h=$ 1.1 m 时,立刻启动返回舱的缓冲发动机并向下喷气,舱体再次做减速运动,经历时间 $t=0.2 \mathrm{~s}$ 后,以某一安全的速度落至地面。设最后的减速过程可视为坚直方向的匀减速直线运动,取 $g=10 \mathrm{~m} / \mathrm{s}^2$ ,则最后减速过程中
$\text{A.}$ 返回舱中的航天员处于失重状态
$\text{B.}$ 返回舱加速度大小为 $25 \mathrm{~m} / \mathrm{s}^2$
$\text{C.}$ 返回舱落地的瞬间速度大小为 $2 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 返回舱对质量 $m=60 \mathrm{~kg}$ 的航天员的作用力的大小为 2700 N
为了是雨滴尽可能淌离屋顶,要设计好房顶的高度,设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么如图所示的四种情况中符合要求的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
如图所示,$O a 、 O b$ 和 $a d$ 是坚直平面内三根固定的光滑细杆,$O$ 、 $a 、 b 、 c$ 、 $d$ 位于同一圆周上,$c$ 为圆周的最高点,$a$ 为最低点,$O^{\prime}$ 为圆心。每根杆上都套着一个小滑环(未画出),两个滑环从 $O$ 点无初速释放,一个滑环从 $d$ 点无初速释放,用 $t_1$ 、 $t_2 、 t_3$ 分别表示滑环沿 $O a 、 O b 、 d a$ 到达 $a 、 b$所用的时间,则下列关系正确的是
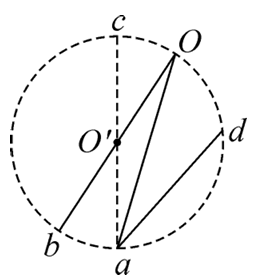
$\text{A.}$ $t_1=t_2$
$\text{B.}$ $t_2>t_3$
$\text{C.}$ $t_1 < t_2$
$\text{D.}$ $t_1=t_3$
如图甲所示,物块的质量 $m=1 \mathrm{~kg}$ ,初速度 $v_0=10 \mathrm{~m} / \mathrm{s}$ ,在一水平向左的恒力 $F$ 作用下从 $O$ 点沿粗糙的水平面向右运动,某时刻 $F$突然反向,大小不变,整个过程中物块速度的平方随位置坐标变化的关系图像如图乙所示,$g=10 \mathrm{~m} / \mathrm{s}^2$ 。下列说法中正确的是
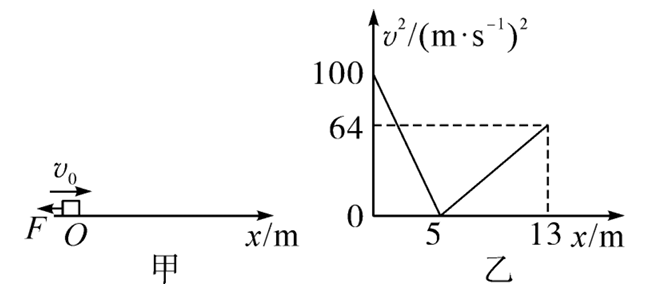
$\text{A.}$ $0 \sim 5 \mathrm{~m}$ 内物块做匀减速运动
$\text{B.}$ 在 $t=1 \mathrm{~s}$ 时刻,恒力 $F$ 反向
$\text{C.}$ 恒力 $F$ 大小为 10 N
$\text{D.}$ 物块与水平面间的动摩擦因数为 0.3
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
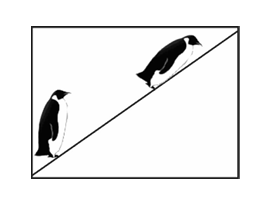
可爱的企鹅喜欢在冰面上玩游戏。如图所示,有一企鹅在倾角为 $37^{\circ}$ 的倾斜冰面上,先以加速度 $a=0.5 \mathrm{~m} / \mathrm{s}^2$ 从冰面底部由静止开始沿直线向上"奔跑",$t=8 \mathrm{~s}$ 时,突然卧倒以肚皮贴着冰面向前滑行,最后退滑到出发点,完成一次游戏(企鹅在滑动过程中姿势保持不变)。若企鹅肚皮与冰面间的动摩擦因数 $\mu=0.25$ ,已知 $\sin 37^{\circ}=0.6$ , $\cos 37^{\circ}=0.8, g=10 \mathrm{~m} / \mathrm{s}^2$ 。求:
(1)企鹅向上"奔跑"的位移大小;
(2)企鹅在冰面滑动的加速度大小;
(3)企鹅退滑到出发点时的速度大小。(计算结果可用根式表示)
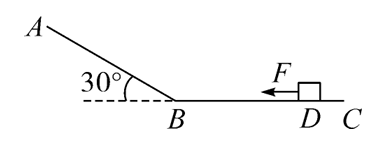
光滑斜面 $A B$ 与一粗糙水平面 $B C$ 连接,斜面倾角 $\theta=30^{\circ}$ ,质量 $m=2 \mathrm{~kg}$ 的物体置于水平血上的 $D$ 点,$D B$ 间的距离 $d=7 \mathrm{~m}$ ,物体与水平面间的动摩擦因数 $\mu=0.2$ ,将一水平向左的恒力 $F=8 \mathrm{~N}$ 作用在该物体上, $t=2 \mathrm{~s}$ 后撤去该力,不考虑物体经过 $B$ 点点时的速度损失。求撤去拉力 $F$ 后,经过多长时间物体经过 $B$ 点?
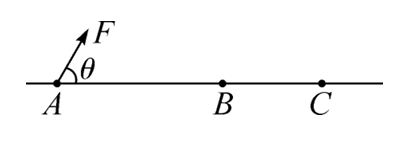
如图所示,直杆水平固定,质量为 $m=$ 0.1 kg 的小圆环(未画出)套在杆上 $A$ 点,在坚直平面内对环施加一个与杆夹角为 $\theta=53^{\circ}$ 的斜向上的拉力 $F$ ,使小圆环由静止开始沿杆向右运动,并在经过 $B$ 点时撤掉此拉力 $F$ ,小圆环最终停在 $C$ 点。已知小圆环与直杆间的动摩擦因数 $\mu=0.8, ~ A B$ 与 $B C$的距离之比 $s_1: s_2=8: 5$ 。( $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$ , $\sin 53^{\circ}=0.8, ~ \cos 53^{\circ}=0.6$ )求:
(1)小圆环在 $B C$ 段的加速度 $a_2$ 的大小;
(2)小圆环在 $A B$ 段的加速度 $a_1$ 的大小;
(3)拉力 $F$ 的大小。