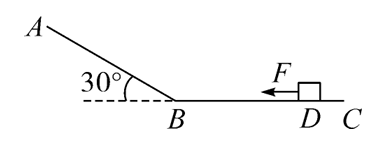
光滑斜面 $A B$ 与一粗糙水平面 $B C$ 连接,斜面倾角 $\theta=30^{\circ}$ ,质量 $m=2 \mathrm{~kg}$ 的物体置于水平血上的 $D$ 点,$D B$ 间的距离 $d=7 \mathrm{~m}$ ,物体与水平面间的动摩擦因数 $\mu=0.2$ ,将一水平向左的恒力 $F=8 \mathrm{~N}$ 作用在该物体上, $t=2 \mathrm{~s}$ 后撤去该力,不考虑物体经过 $B$ 点点时的速度损失。求撤去拉力 $F$ 后,经过多长时间物体经过 $B$ 点?