单选题 (共 6 题 ),每题只有一个选项正确
在某个恶劣天气中,能见度很低,甲、乙两汽车在一条平直的单行道上,甲在前、乙在后同向行驶。某时刻两车司机听到前方有事故发生的警笛提示,同时开始刹车,两车刹车后的 $v-t$ 图像如图所示,下列说法正确的是
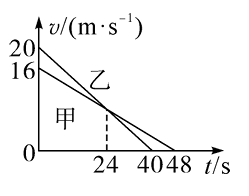
$\text{A.}$ 甲车的加速度大于乙车的加速度
$\text{B.}$ 若 $t=24 \mathrm{~s}$ 时两车未发生碰撞,则此时两车相距最远
$\text{C.}$ 为避免两车发生碰撞,开始刹车时两车的间距至少为 48 m
$\text{D.}$ 若两车发生碰撞,则可能是在开始刹车 24 s 以后的某时刻发生的
甲、乙两辆玩具车在同一平直路面上行驶,二者运动的位移-时间图像如图所示,其中乙车的位移-时间图线是关于 $x$ 轴对称的抛物线的一部分,则下列说法正确的是
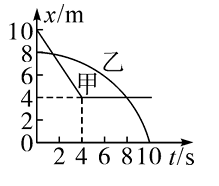
$\text{A.}$ 甲车先做匀减速直线运动后做匀速直线运动
$\text{B.}$ 乙车一定做初速度为零的匀加速直线运动
$\text{C.}$ 甲车在 $0 \sim 10 \mathrm{~s}$ 内的平均速度为 $-1.5 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 在 $0 \sim 10 \mathrm{~s}$ 内甲、乙两车相遇两次,且相遇时速度可能相等
假设高速公路上甲、乙两车在同一车道上同向行驶。甲车在前,乙车在后。速度均为 $v_0=30 \mathrm{~m} / \mathrm{s}$ 。甲、乙相距 $x_0=100 \mathrm{~m}, t=0$时刻甲车遇紧急情况后,甲、乙两车的加速度随时间变化如图甲、乙所示,取运动方向为正方向。下列说法正确的是
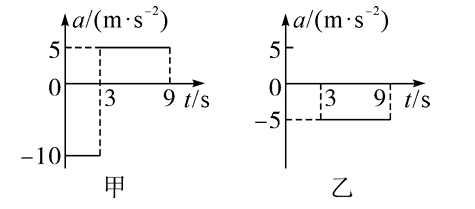
$\text{A.}$ $t=3 \mathrm{~s}$ 时两车相距最近
$\text{B.}$ $t=6 \mathrm{~s}$ 时两车速度不相等
$\text{C.}$ $t=6 \mathrm{~s}$ 时两车距离最近,且最近距离为 10 m
$\text{D.}$ 两车在 $0 \sim 9 \mathrm{~s}$ 内会相撞
在某个恶劣天气中,能见度很低,甲、乙两汽车在一条平直的单行道上,甲在前、乙在后同向行驶。某时刻两车司机听到前方有事故发生的警笛提示,同时开始刹车,两车刹车后的 $v-t$ 图像如图所示,下列说法正确的是
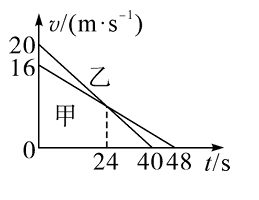
$\text{A.}$ 甲车的加速度大于乙车的加速度
$\text{B.}$ 若 $t=24 \mathrm{~s}$ 时两车未发生碰撞,则此时两车相距最远
$\text{C.}$ 为避免两车发生碰撞,开始刹车时两车的间距至少为 48 m
$\text{D.}$ 若两车发生碰撞,则可能是在开始刹车 24 s 以后的某时刻发生的
甲、乙两辆玩具车在同一平直路面上行驶,二者运动的位移-时间图像如图所示,其中乙车的位移-时间图线是关于 $x$ 轴对称的抛物线的一部分,则下列说法正确的是
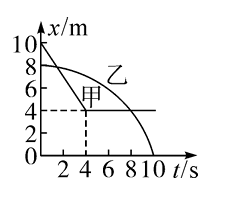
$\text{A.}$ 甲车先做匀减速直线运动后做匀速直线运动
$\text{B.}$ 乙车一定做初速度为零的匀加速直线运动
$\text{C.}$ 甲车在 $0 \sim 10 \mathrm{~s}$ 内的平均速度为 $-1.5 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 在 $0 \sim 10 \mathrm{~s}$ 内甲、乙两车相遇两次,且相遇时速度可能相等
假设高速公路上甲、乙两车在同一车道上同向行驶。甲车在前,乙车在后。速度均为 $v_0=30 \mathrm{~m} / \mathrm{s}$ 。甲、乙相距 $x_0=100 \mathrm{~m}, t=0$时刻甲车遇紧急情况后,甲、乙两车的加速度随时间变化如图甲、乙所示,取运动方向为正方向。下列说法正确的是
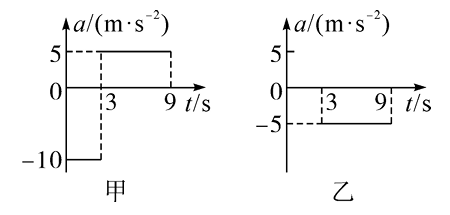
$\text{A.}$ $t=3 \mathrm{~s}$ 时两车相距最近
$\text{B.}$ $t=6 \mathrm{~s}$ 时两车速度不相等
$\text{C.}$ $t=6 \mathrm{~s}$ 时两车距离最近,且最近距离为 10 m
$\text{D.}$ 两车在 $0 \sim 9 \mathrm{~s}$ 内会相撞
多选题 (共 2 题 ),每题有多个选项正确
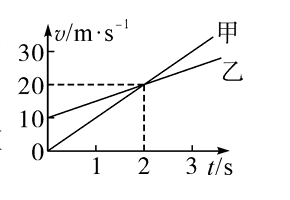
甲、乙两车在平直公路上同向行驶,其 $v-t$图像如图所示。已知两车在 $t=3 \mathrm{~s}$ 时并排行驶,则
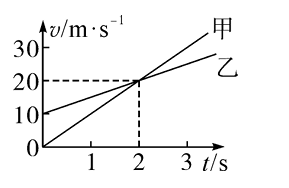
$\text{A.}$ 在 $t=0$ 时,甲车在乙车前 7.5 m
$\text{B.}$ 在 $t=1 \mathrm{~s}$ 时,甲车在乙车后
$\text{C.}$ 两车另一次并排行驶的时刻是 $t=2 \mathrm{~s}$
$\text{D.}$ 甲、乙车两次并排行驶的位置之间沿公路方向的距离为 40 m
甲、乙两车在平直公路上同向行驶,其 $v-t$图像如图所示。已知两车在 $t=3 \mathrm{~s}$ 时并排行驶,则
$\text{A.}$ 在 $t=0$ 时,甲车在乙车前 7.5 m
$\text{B.}$ 在 $t=1 \mathrm{~s}$ 时,甲车在乙车后
$\text{C.}$ 两车另一次并排行驶的时刻是 $t=2 \mathrm{~s}$
$\text{D.}$ 甲、乙车两次并排行驶的位置之间沿公路方向的距离为 40 m
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
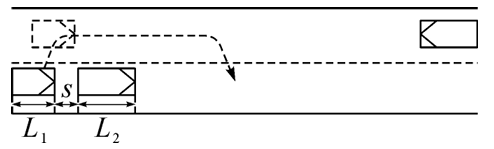
强行超车是道路交通安全的极大隐患之一、如图是汽车超车过程的示意图,汽车甲和货车均以 $36 \mathrm{~km} / \mathrm{h}$ 的速度在平直路面上匀速行驶,其中甲车车身长 $L_1=4 \mathrm{~m}$ 、货车车身长 $L_2 =4 \mathrm{~m}$ ,货车在甲车前 $s=4 \mathrm{~m}$ 。若甲车司机发现附近无其他车辆后开始加速从货车左侧超车,加速度大小为 $2 \mathrm{~m} / \mathrm{s}^2$ 。假定货车速度保持不变,汽车车尾超过货车车头 4 m 后完成超车,不计车辆变道的时间及车辆的宽度。求:
(1)甲车完成超车至少需要多长时间;
(2)若甲车开始超车时,看到道路正前方的乙车迎面驶来,此时二者相距 110 m ,乙车速度为 $54 \mathrm{~km} / \mathrm{h}$ 。甲车超车的整个过程中,乙车速度始终保持不变,请通过计算分析,甲车能否安全超车。
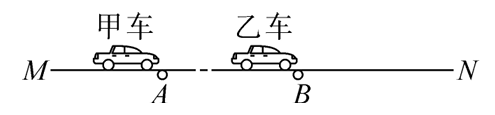
如图所示,直线 $M N$ 表示一条平直单车道,甲、乙两辆汽车刚开始静止,车头分别在 $A 、 B$两处,两辆车长均为 $L=4 \mathrm{~m}$ ,两个车头间的距离为 $x_0=89 \mathrm{~m}$ ,现甲车先开始向右做匀加速直线运动,加速度 $a_1=2.5 \mathrm{~m} / \mathrm{s}^2$ ,甲车运动了 $t_0=5 \mathrm{~s}$ 后,发现乙车仍然静止,甲车立即鸣笛,又经过 $t_1=1 \mathrm{~s}$ ,乙车才开始向右做匀加速直线运动。
(1)若乙车运动的加速度 $a_2=5.0 \mathrm{~m} / \mathrm{s}^2$ ,两辆汽车是否会相撞?通过计算说明。
(2)若要使两车不相撞,乙车运动的加速度至少是多少?
某一长直的赛道上,一辆 F1 赛车前方 200 m处有一安全车正以 $10 \mathrm{~m} / \mathrm{s}$ 的速度匀速前进,这时赛车从静止出发以 $2 \mathrm{~m} / \mathrm{s}^2$ 的加速度追赶。
(1)求赛车出发 3 s 末的瞬时速度大小;
(2)赛车何时追上安全车?追上之前与安全车最远相距多少米?
(3)当赛车刚追上安全车时,赛车手立即刹车,使赛车以 $4 \mathrm{~m} / \mathrm{s}^2$ 的加速度做匀减速直线运动,问两车再经过多长时间第二次相遇? (设赛车可以从安全车旁经过而不发生相碰)
汽车 A 以 $v_{\mathrm{A}}=4 \mathrm{~m} / \mathrm{s}$ 的速度向右做匀速直线运动,发现前方相距 $x_0=7 \mathrm{~m}$ 处、以 $v_{\mathrm{B}}= 10 \mathrm{~m} / \mathrm{s}$ 的速度同向运动的汽车 B 正开始匀减速刹车直到静止后保持不动,其刹车的加速度大小 $a=2 \mathrm{~m} / \mathrm{s}^2$ 从此刻开始计时。求:
(1) A 追上 B 前, A 、 B 间的最远距离是多少?
(2)经过多长时间 A 恰好追上 B ?
【拓展延伸】(1)若某同学应用关系式 $v_B t- \frac{1}{2} a t^2+x_0=v_{\mathrm{A}} t$ ,解得经过 $t=7 \mathrm{~s}$(另解舍去)时 A 恰好追上 B 。这个结果合理吗?为什么? (2)若汽车 A 以 $v_{\mathrm{A}}=4 \mathrm{~m} / \mathrm{s}$ 的速度向左匀速运动,其后方相距 $x_0=7 \mathrm{~m}$ 处,以 $v_{\mathrm{B}}=10 \mathrm{~m} / \mathrm{s}$ 的速度同方向运动的汽车 B 开始匀减速刹车直到静止后保持不动,其刹车的加速度大小为 $a= 2 \mathrm{~m} / \mathrm{s}^2$ ,则经过多长时间两车恰好相遇?
一汽车在直线公路段上以 $54 \mathrm{~km} / \mathrm{h}$ 的速度匀速行驶,突然发现在其正前方 14 m 处有一辆自行车以 $5 \mathrm{~m} / \mathrm{s}$ 的速度同向匀速行驶。经过 0.4 s 的反应时间后,司机开始刹车,则:
(1)为了避免相撞,汽车的加速度大小至少为多少?
(2)若汽车刹车时的加速度只为 $4 \mathrm{~m} / \mathrm{s}^2$ ,在汽车开始刹车的同时自行车开始以一定的加速度匀加速,则自行车的加速度至少为多大才能保证两车不相撞?
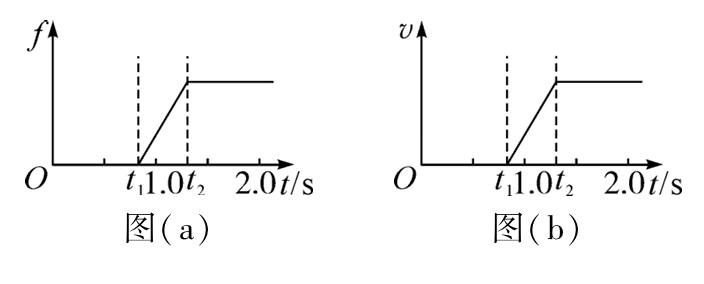
(2019-全国卷 II)一质量为 $m=2000 \mathrm{~kg}$ 的汽车以某一速度在平直公路上匀速行驶。行驶过程中,司机忽然发现前方 100 m 处有一警示牌。立即刹车,刹车过程中,汽车所受阻力大小随时间变化可简化为图(a)中的图线。图(a)中, $0 \sim t_1$ 时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),$t_1=0.8 \mathrm{~s} ; t_1 \sim t_2$ 时间段为刹车系统的启动时间,$t_2=1.3 \mathrm{~s}$ ;从 $t_2$ 时刻开始汽车的刹车系统稳定工作,直至汽车停止,已知从 $t_2$ 时刻开始,汽车第 1 s 内的位移为 24 m ,第 4 s 内的位移为 1 m 。
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的 $v-t$图线;
(2)求 $t_2$ 时刻汽车的速度大小及此后的加速度大小;
如图所示是某一次接力训练。已知甲、乙两运动员经短距离加速后都能达到并保持 10 $\mathrm{m} / \mathrm{s}$ 的速度跑完全程。设乙从起跑后到接棒前的运动是匀加速的,加速度大小为 $3 \mathrm{~m} / \mathrm{s}^2$ 。乙在接力区前端听到口令时起跑,在甲、乙相遇时完成交接棒。在某次练习中,甲以 $v= 10 \mathrm{~m} / \mathrm{s}$ 的速度跑到接力区前端 $x_0=14.0 \mathrm{~m}$处向乙发出起跑口令。已知接力区的长度为 $L=20 \mathrm{~m}$ 。求:
(1)此次练习中交接棒处离接力区前端(即乙出发的位置)的距离;
(2)为了达到理想成绩,需要乙恰好在速度达到与甲相同时被甲追上,则甲应在接力区前端多远时对乙发出起跑口令;
(3)在(2)中,棒经过接力区的时间是多少?