单选题 (共 4 题 ),每题只有一个选项正确
已知 $a=\sqrt{5}+2, b=\sqrt{5}-2$ ,则 $\sqrt{a^2+b^2+7}$ 的值为
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 3
$\text{D.}$ 4
已知 $a=2+2 \sqrt{2}, b=2-2 \sqrt{2}$ ,则 $\frac{1}{a}+\frac{1}{b}$ 的值为
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $-\sqrt{2}$
已知 $a+b=\sqrt{2}-1, a b=-1$ ,则 $a^2+a b+b^2$ 的值是
$\text{A.}$ $2-\sqrt{2}$
$\text{B.}$ $4-2 \sqrt{2}$
$\text{C.}$ $2-2 \sqrt{2}$
$\text{D.}$ $3-\sqrt{2}$
已知 $a=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}, b=\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}$ ,则二次根式 $\sqrt{a^3 b+a b^3+19}$ 的值是
$\text{A.}$ 6
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 9
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知 $a+b=6, a b=7$ ,则代数式 $a \sqrt{\frac{a}{b}}+b \sqrt{\frac{b}{a}}$ 的值
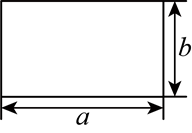
边长为 $a, b$ 的长方形如图所示,若它的周长为 $2+2 \sqrt{5}$ ,面积为 $\sqrt{5}$ ,则 $a^2 b+a b^2$ 的值为
人们把 $\frac{\sqrt{5}-1}{2}$ 这个数叫做黄金分割数,著名数学家华罗庚的优选法中的 0.618 就应用了黄金分割数.设 $a=\frac{\sqrt{5}+1}{2}, b=\frac{\sqrt{5}-1}{2}$ ,记 $S_1=\frac{1}{1+a}+\frac{1}{1+b}, S_2=\frac{2}{1+a^2}+\frac{2}{1+b^2}, \ldots \ldots$ , $S_{20}=\frac{20}{1+a^{20}}+\frac{20}{1+b^{20}}$ ,则 $S_1+S_2+\cdots+S_{20}$ 的值为
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $x=\frac{1}{2}(\sqrt{5}+\sqrt{3}), y=\frac{1}{2}(\sqrt{5}-\sqrt{3})$ ,则 $\frac{x}{y}+\frac{y}{x}$ 的值是
已知 $a=\sqrt{3}+\sqrt{2}, b=\sqrt{3}-\sqrt{2}$ .
(1)求 $a^2+b^2$ 的值;
(2)求 $\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}$ 的值.
已知 $x+y=-5, x y=4$ ,求 $x \sqrt{\frac{y}{x}}+y \sqrt{\frac{x}{y}}$ 的值