单选题 （共 8 题 ），每题只有一个选项正确
下列图形中，既是轴对称图形又是中心对称图形的是
$\text{A.}$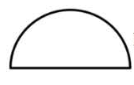 
$\text{B.}$ 
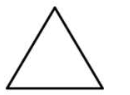$\text{C.}$ 
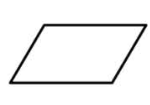$\text{D.}$ 
实数 $a, b$ 在数轴上的对应点的位置如图所示，下列结论中正确的是
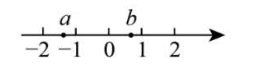
$\text{A.}$ $a>-1$
$\text{B.}$ $a+b=0$
$\text{C.}$ $a-b>0$
$\text{D.}$ $|a|>|b|$
若一个六边形的每个内角都是 $x^{\circ}$ ，则 $x$ 的值为（ ）
$\text{A.}$ 60
$\text{B.}$ 90
$\text{C.}$ 120
$\text{D.}$ 150
一个不透明的袋子中仅有 3 个红球、 2 个黄球和 1 个白球，这些球除颜色外无其他差别．从袋子中随机摸出一个球，摸出的球是白球的概率是
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{5}{6}$
若关于 $x$ 的一元二次方程 $a x^2+2 x+1=0$ 有两个相等的实数根，则实数 $a$ 的值为
$\text{A.}$ -4
$\text{B.}$ -1
$\text{C.}$ 1
$\text{D.}$ 4
6． 2025 年 5 月 29 日，行星探测工程天问二号探测器在西昌卫星发射中心成功发射，开启对近地小行星 2016 HO 3 的探测与采样返回之旅．已知该小行星与地球的最近距离约为月球远地点距离的 45 倍，月球远地点距离约为 $4 \times 10^5 \mathrm{~km}$ ，则该小行星与地球的最近距离约为（ ）
$\text{A.}$ $1.8 \times 10^5 \mathrm{~km}$
$\text{B.}$ $1.8 \times 10^6 \mathrm{~km}$
$\text{C.}$ $1.8 \times 10^7 \mathrm{~km}$
$\text{D.}$ $1.8 \times 10^{10} \mathrm{~km}$
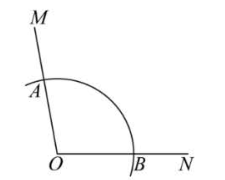
如图，$\angle M O N=100^{\circ}$ ，点 $A$ 在射线 $O M$ 上，以点 $O$ 为圆心，$O A$ 长为半径画弧，交射线 $O N$于点 $B$ ．若分别以点 $A, B$ 为圆心，$A B$ 长为半径画弧，两弧在 $\angle M O N$ 内部交于点 $C$ ，连接 $A C$ ，则 $\angle O A C$ 的大小为
$\text{A.}$ $80^{\circ}$
$\text{B.}$ $100^{\circ}$
$\text{C.}$ $110^{\circ}$
$\text{D.}$ $120^{\circ}$
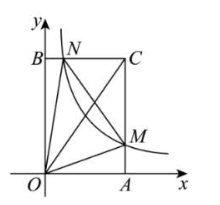
如图，在平面直角坐标系 $x O y$ 中， $\mathrm{A}, B$ 分别是横、纵轴正半轴上的动点，四边形 $O A C B$是矩形，函数 $y=\frac{1}{x}(x>0)$ 的图象与边 $A C$ 交于点 $M$ ，与边 $B C$ 交于点 $N(M, N$ 不重合）．给出下面四个结论：
（1）$\triangle C O M$ 与 $\triangle C O N$ 的面积一定相等；
（2）$\triangle M O N$ 与 $\triangle M C N$ 的面积可能相等；
（3）$\triangle M O N$ 一定是锐角三角形；
（4）$\triangle M O N$ 可能是等边三角形．
上述结论中，所有正确结论的序号是
$\text{A.}$ （1）（3）
$\text{B.}$ （1）（4）
$\text{C.}$ （2）（3）
$\text{D.}$ （2）（4）
填空题 （共 8 题 ），请把答案直接填写在答题纸上
若 $\sqrt{3 x-3}$ 在实数范围内有意义，则实数 $x$ 的取值范围是．
方程 $\frac{2}{x-6}+\frac{1}{x}=0$ 的解为．
某地区七年级共有 2000 名男生．为了解这些男生的体重指数（BMI）分布情况，从中随机抽取了 100 名男生，测得他们的 BMI 数据（单位： $\mathrm{kg} / \mathrm{m}^2$ ），并根据七年级男生体质健康标准整理如下：
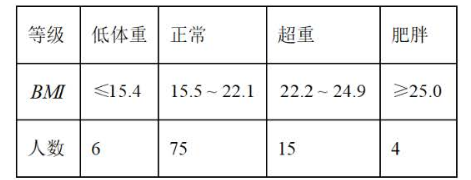
根据以上信息，估计该地区七年级 2000 名男生中 $B M I$ 等级为正常的人数是．
能说明命题＂若 $a^2>4 b^2$ ，则 $a>2 b$＂是假命题的一组实数 $a, b$ 的值为 $a=, b=$ ．
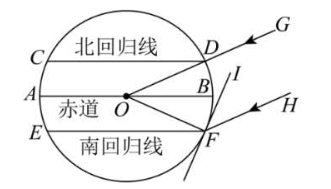
如图，$\odot O$ 是地球的示意图，其中 $A B$ 表示赤道，$C D, E F$ 分别表示北回归线和南回归线，$\angle D O B=\angle F O B=23.5^{\circ}$ ．夏至日正午时，太阳光线 $G D$ 所在直线经过地心 $O$ ，此时点 $F$处的太阳高度角 $\triangle I F H$（即平行于 $G D$ 的光线 $H F$ 与 $\odot O$ 的切线 $F I$ 所成的锐角）的大小为 ${ }^{\circ}$ ．
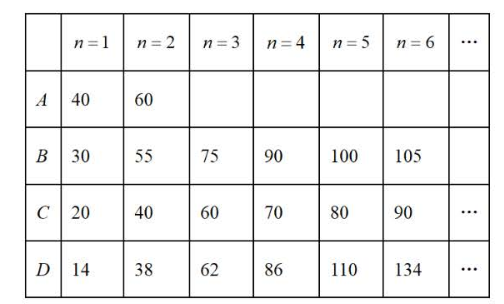
如图，在正方形 $A B C D$ 中，点 $E$ 在边 $C D$ 上，$C F \perp B E$ ，垂足为 $F$ ．若 $A B=1, \angle E B C=30^{\circ}$ ，则 $\triangle A B F$ 的面积为．
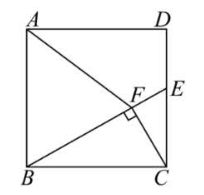
某企业研发并生产了一种新设备，计划分配给 $A, B, C, D$ 四家经销商销售．当一家经销商将分配到的 $n$ 台设备全部售出后，企业从该经销商处获得的利润（单位：万元）与 $n$的对应关系如下：
（1）如果企业将 5 台设备分配给这四家经销商销售，且每家经销商至少分配到 1 台设备，为使 5 台设备都售出后企业获得的总利润最大，应向经销商分配 2 台设备（填＂$A$＂＂$B$＂＂$C$＂或＂$D$＂）；
（2）如果企业将 6 台设备分配给这四家经销商中的一家或多家销售，那么 6 台设备都售出后，企业可获得的总利润的最大值为万元．
解答题 （共 12 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算：$|-3|+\sqrt{27}+\left(\frac{1}{2}\right)^{-1}-2 \sin 30^{\circ}$ ．
解不等式组：$\left\{\begin{array}{l}2(x+1)>x-1 \\ \frac{x+5}{2}>3 x\end{array}\right.$
已知 $a+b-3=0$ ，求代数式 $\frac{4(a-b)+8 b}{a^2+2 a b+b^2}$ 的值．
如图，在 $\triangle A B C$ 中，$D, E$ 分别为 $A B, A C$ 的中点，$D F \perp B C$ ，垂足为 $F$ ，点 $G$ 在 $D E$的延长线上，$D G=F C$ ．
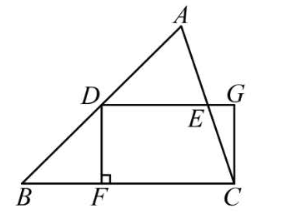
（1）求证：四边形 $D F C G$ 是矩形；
（2）若 $\angle B=45^{\circ}, D F=3, D G=5$ ，求 $B C$ 和 $A C$ 的长．
在平面直角坐标系 $x O y$ 中，函数 $y=k x+b(k \neq 0)$ 的图象经过点 $(1,3)$ 和 $(2,5)$ ．
（1）求 $k, b$ 的值；
（2）当 $x < 1$ 时，对于 $x$ 的每一个值，函数 $y=m x(m \neq 0)$ 的值既小于函数 $y=k x+b$ 的值，也小于函数 $y=x+k$ 的值，直接写出 $m$ 的取值范围．
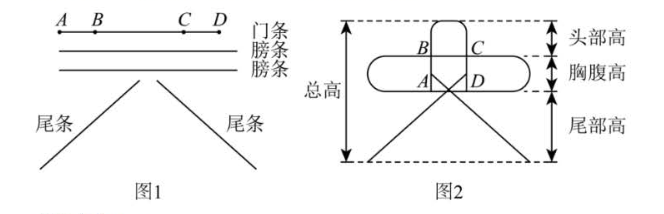
北京风筝制作技艺是国家级非物质文化遗产．为制作一只京燕风筝，小明准备了五根直竹条（如图 1）：一根门条、两根等长的膀条和两根等长的尾条．他将门条和膀条分别烤弯后与尾条一起扎成风筝的骨架（如图2），其头部高、胸腹高与尾部高的比是 $1: 1: 2$ ．已知单根膀条长是胸腹高的 5 倍，门条比单根膀条短 10 cm ，图 1 中 $B C$ 的长是门条长的 $\frac{5}{9}, A B, C D$的长均等于胸腹高．求这只风筝的骨架的总高．
校田径队教练选出甲、乙、丙、丁四名运动员参加 100 米比赛．对这四名运动员最近10 次 100 米跑测试成绩（单位：s）的数据进行整理、描述和分析．下面给出了部分信息．
a．甲、乙两名运动员 10 次测试成绩的折线图：
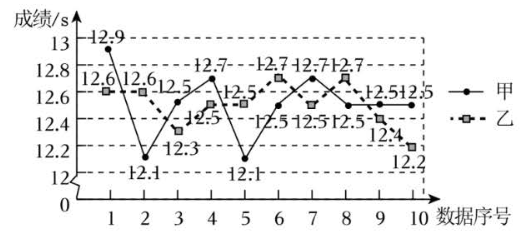
b．丙运动员 10 次测试成绩：
12.4 12.4 12.5 12.7 12.8 12.8 12.8 12.8 12.9 12 .9
c．四名运动员 10 次测试成绩的平均数、中位数、方差：
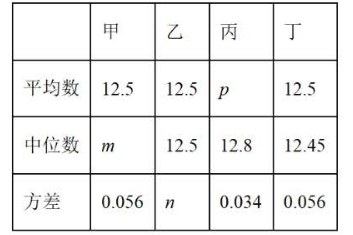
（1）表中 $m$ 的值为 $\_\_\_\_$ ；
（2）表中 $n$ $\_\_\_\_$ 0.056 （填＂＞＂＂＝＂或＂＜＂）；
（3）根据这 10 次测试成绩，教练按如下方式评估这四名运动员的实力强弱：首先比较平均数，平均数较小者实力更强；若平均数相等，则比较方差，方差较小者实力更强；若平均数、方差分别相等，则测试成绩小于平均数的次数较多者实力更强．
评估结果：这四名运动员按实力由强到弱依次为 $\_\_\_\_$ ．
如图，过点 $P$ 作 $\odot O$ 的两条切线，切点分别为 $A, B$ ，连接 $O A, O B, O P$ ，取 $O P$ 的中点 $C$ ，连接 $A C$ 并延长，交 $\odot O$ 于点 $D$ ，连接 $B D$ ．
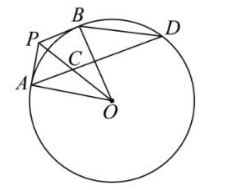
（1）求证：$\angle A D B=\angle A O P$ ；
（2）延长 $O P$ 交 $D B$ 的延长线于点 $E$ ．若 $A P=10, \tan \angle A O P=\frac{1}{2}$ ，求 $D E$ 的长．
工厂对新员工进行某种工艺品制作的培训．在完成理论学习后，新员工接下来先使用智能辅助训练系统进行一次为期 $T$ 日（ $T$ 可取 $0,1,2$ 或 3 ）的模拟练习，然后开始试制．记一名新员工在试制阶段的第 $x$ 日单日制成的合格品的个数为 $y$ ，根据以往的培训经验，对于给定的 $T$ ，可以认为 $y$ 是 $x$ 的函数．当 $T=0$ 和 $T=3$ 时，部分数据如下：
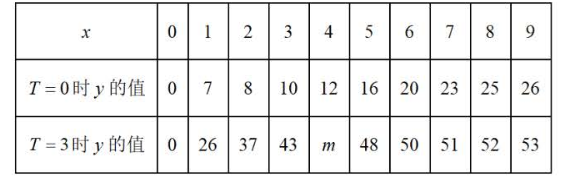
$T=3$ 时，从试制阶段的第2日起，一名新员工每一日比前一日多制成的合格品的个数逐渐减少或保持不变．
对于给定的 $T$ ，在平面直角坐标系 $x O y$ 中描出该 $T$ 值下各数对 $(x, y)$ 所对应的点，并根据变化趋势用平滑曲线连接，得到曲线 $C_T$ ．当 $T=1$ 和 $T=2$ 时，曲线 $C_1, C_2$ 如图所示．
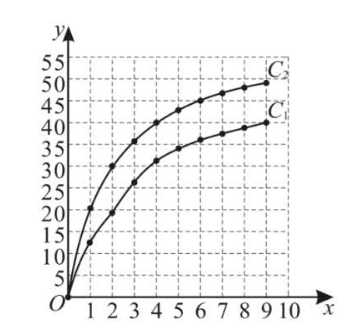
（1）观察曲线 $C_1$ ，当整数 $x$ 的值为 $\_\_\_\_$时，$y$ 的值首次超过 35；
（2）写出表中 $m$ 的值，并在给出的平面直角坐标系中画出 $T=3$ 时的曲线 $C_3$ ；
（3）新员工小云和小腾刚刚完成理论学习，接下来进行模拟练习和试制．
① 若新员工单日制成不少于 45 个合格品即可获得＂优秀学员＂证书，根据上述函数关系，小云最早在完成理论学习后的第 $\_\_\_\_$日可获得＂优秀学员＂证书；
② 若工厂希望小腾在完成理论学习后的 4 日内制成的合格品的总数最多，根据上述函数关系，
在这 4 日中应安排小腾先进行 $\_\_\_\_$日的模拟练习。
在平面直角坐标系 $x O y$ 中，拋物线 $y=a x^2+b x+c(a \neq 0)$ 经过点 $O$ 和点 $A(3,3 a)$ ．
（1）求 $c$ 的值，并用含 $a$ 的式子表示 $b$ ；
（2）过点 $P(t, 0)$ 作 $x$ 轴的垂线，交抛物线于点 $M$ ，交直线 $y=a x$ 于点 $N$ ．
① 若 $a=1, t=4$ ，求 $M N$ 的长；
② 已知在点 $P$ 从点 $O$ 运动到点 $B(2 a, 0)$ 的过程中，$M N$ 的长随 $O P$ 的长的增大而增大，求 $a$的取值范围．
在 $\triangle A B C$ 中，$\angle A C B=90^{\circ}, \angle A B C=\alpha$ ，点 $D$ 在射线 $B C$ 上，连接 $A D$ ，将线段 $A D$ 绕点 A 逆时针旋转 $180^{\circ}-2 \alpha$ 得到线段 $A E$（点 $E$ 不在直线 $A B$ 上），过点 $E$ 作 $E F / / A B$ ，交直线 $B C$ 于点 $F$ ．
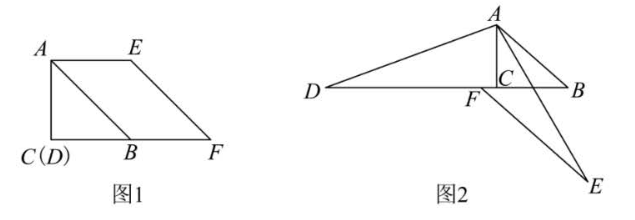
（1）如图 1，$\alpha=45^{\circ}$ ，点 $D$ 与点 $C$ 重合，求证：$B F=A C$ ；
（2）如图 2，点 $D, F$ 都在 $B C$ 的延长线上，用等式表示 $D F$ 与 $B C$ 的数量关系，并证明．
在平面直角坐标系 $x O y$ 中，对于点 A 和 $\odot C$ 给出如下定义：若 $\odot C$ 上存在两个不同的点 $M, N$ ，对于 $\odot C$ 上任意满足 $A P=A Q$ 的两个不同的点 $P, Q$ ，都有 $\angle P A Q \leq \angle M A N$ ，则称点 A 是 $\odot C$ 的关联点，称 $\angle M A N$ 的大小为点 A 与 $\odot C$ 的关联角度．（本定义中的角均指锐角、直角、钝角或平角）
（1）如图，$\odot O$ 的半径为 1 ．
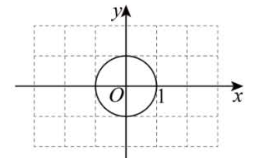
（1）在点 $A_1\left(\frac{1}{2}, 0\right), A_2\left(\frac{4}{3}, 0\right), A_3(2,0)$ 中，点 $\_\_\_\_$是 $\odot O$ 的关联点且其与 $\odot O$ 的关联角度小于 $90^{\circ}$ ，该点与 $\odot O$ 的关联角度为 $\_\_\_\_$ ${ }^{\circ}$ ；
（2）点 $B(1, m)$ 在第一象限，若对于任意长度小于 1 的线段 $B D, B D$ 上所有的点都是 $\odot O$ 的关联点，则 $m$ 的最小值为 $\_\_\_\_$ ；
（2）已知点 $E(1,3), F(4,3), T(t, 0), \odot T$ 经过原点，线段 $E F$ 上所有的点都是 $\odot T$ 的关联点，记这些点与 $\odot T$ 的关联角度的最大值为 $\alpha$ ．若 $90^{\circ} \leq \alpha \leq 180^{\circ}$ ，直接写出 $t$ 的取值范围．