单选题 (共 3 题 ),每题只有一个选项正确
如图所示,在光滑的水平地面上有一静止的质量为M的四分之一光滑圆弧滑块,圆弧的半径为R,最低点处刚好与水平地面相切.一质量为m的小球以一定的初速度v0沿水平地面向右运动,不计小球冲上圆弧滑块过程中的机械能损失.如果圆弧滑块固定,则小球恰能冲到圆弧面上与圆心等高处;如果圆弧滑块不固定,则小球在圆弧面上能到达的最大高度为 .则小球与滑块质量之比m∶M为

$\text{A.}$ 1∶2
$\text{B.}$ 1∶3
$\text{C.}$ 2∶1
$\text{D.}$ 3∶1
如图所示,光滑弧形滑块P锁定在光滑水平地面上,其弧形底端切线水平,小球Q(视为质点)的质量为滑块P的质量的一半,小球Q从滑块P顶端由静止释放,Q离开P时的动能为Ek1.现解除锁定,仍让Q从滑块顶端由静止释放,Q离开P时的动能为Ek2,Ek1和Ek2的比值为
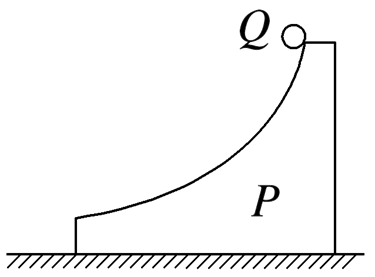
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ $\frac{4}{3}$
如图,在光滑的水平面上静止放一个质量为 $m$ 的木板 $B$ ,木板表面光滑,左端固定一个轻质弹簧。质量为 $2 m$ 的木块 $A$ 以速度 $v_0$ 从板的右端水平向左滑上木板 $B$ 。当木块 $A$ 与弹簧相互作用的过程中,下列判断正确的是
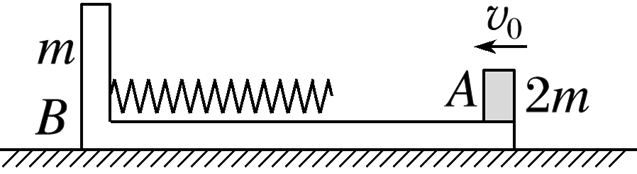
$\text{A.}$ $B$ 板的加速度一直增大
$\text{B.}$ 弹簧压缩量最大时,$B$ 板的速率最大
$\text{C.}$ 弹簧的最大弹性势能为 $\frac{2}{3} m v_0^2$
$\text{D.}$ 弹簧对木块 $A$ 的冲量大小为 $\frac{4}{3} m v_0$
多选题 (共 6 题 ),每题有多个选项正确
如图所示,弹簧一端固定在竖直墙上,质量为m的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量为2m的小球从槽高h处自由下滑,则下列说法正确的是
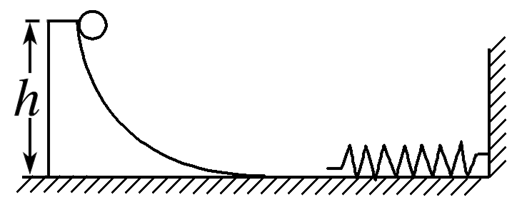
$\text{A.}$ 在下滑过程中,小球和槽组成的系统水平方向上动量守恒
$\text{B.}$ 在下滑过程中,小球和槽组成的系统机械能守恒
$\text{C.}$ 被弹簧反弹后,小球和槽都做速率不变的直线运动
$\text{D.}$ 被弹簧反弹后,小球和槽组成的系统机械能守恒,小球能回到槽高h处
如图所示,质量为M的楔形物体静止在光滑的水平地面上,其斜面光滑且足够长,与水平方向的夹角为θ.一个质量为m的小物块从斜面底端以初速度v0沿斜面向上开始运动.当小物块沿斜面向上运动到最高点时,速度大小为v,距地面高度为h,重力加速度为g,则下列关系式中正确的是
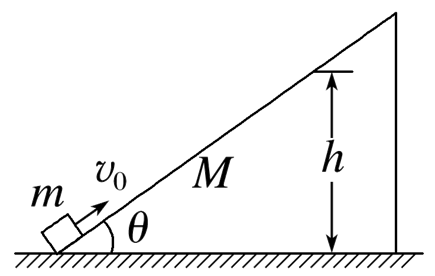
$\text{A.}$ $m v_0=(m+M) v$
$\text{B.}$ $m v_0 \cos \theta=(m+M) v$
$\text{C.}$ $\frac{1}{2} m\left(v_0 \sin \theta\right)^2=m g h$
$\text{D.}$ $\frac{1}{2} m v_0^2=m g h+\frac{1}{2}(m+M) v^2$
如图所示,光滑水平地面上有A、B两物体,质量都为m,B左端固定一个处在压缩状态的轻弹簧,轻弹簧被装置锁定,当弹簧再受到压缩时锁定装置会失效.A以速率v向右运动,当A撞上弹簧后,设弹簧始终不超过弹性限度,关于它们后续的运动过程,下列说法正确的是
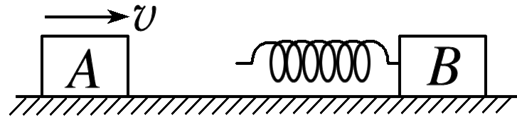
$\text{A.}$ A物体最终会静止,B物体最终会以速率v向右运动
$\text{B.}$ A、B系统的总动量最终将大于mv
$\text{C.}$ A、B系统的总动能最终将大于 mv2
$\text{D.}$ 当弹簧的弹性势能最大时,A、B的总动能为 mv2
如图甲所示,在光滑水平面上,轻质弹簧一端固定,物体 $A$ 以速度 $v_0$ 向右运动压缩弹簧,测得弹簧的最大压缩量为 $x$ .现让弹簧一端连接另一质量为 $m$ 的物体 $B$(如图乙所示),物体 $A$ 以 $2 v_0$ 的速度向右压缩弹簧,测得弹簧的最大压缩量仍为 $x$ ,则
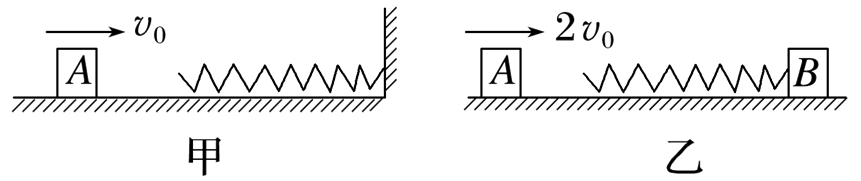
$\text{A.}$ $A$ 物体的质量为 $3 m$
$\text{B.}$ $A$ 物体的质量为 $2 m$
$\text{C.}$ 弹簧压缩最大时的弹性势能为 $\frac{3}{2} m v_0^2$
$\text{D.}$ 弹簧压缩最大时的弹性势能为 $m v_0{ }^2$
如图所示,A、B、C三个半径相等的刚性小球穿在两根平行且光滑的足够长的杆上,三个球的质量分别为mA=2 kg、mB=3 kg、mC=2 kg,初状态三个小球均静止,B、C两球之间连着一根轻质弹簧,弹簧处于原长状态.现给A球一个向左的初速度v0=10 m/s,A、B两球碰后A球的速度变为方向向右、大小为2 m/s.下列说法正确的是
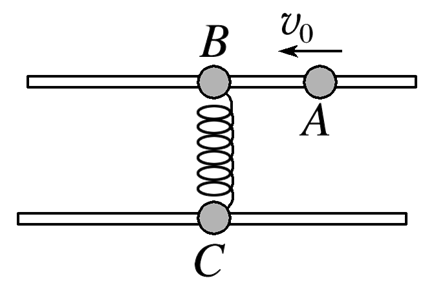
$\text{A.}$ 球A和球B间的碰撞是弹性碰撞
$\text{B.}$ 球A和球B碰后,弹簧恢复到原长时球C的速度大小为9.6 m/s
$\text{C.}$ 球A和球B碰后,球B的最小速度为1.6 m/s
$\text{D.}$ 球A和球B碰后,弹簧的最大弹性势能可以达到96 J
如图所示,光滑水平面上有一质量为 $2 M$ 、半径为 $R(R$ 足够大)的 $\frac{1}{4}$ 圆弧曲面 $C$ ,质量为 $M$ 的小球 $B$ 置于其底端,另一个小球 $A$ 质量为 $\frac{M}{2}$ ,小球 $A$ 以 $v_0=6 m / s$ 的速度向 $B$ 运动,并与 $B$ 发生弹性碰撞,不计一切摩擦,小球均视为质点,则
$\text{A.}$ $B$ 的最大速率为 $4 m / s$
$\text{B.}$ $B$ 运动到最高点时的速率为 $\frac{3}{4} m / s$
$\text{C.}$ $B$ 能与 $A$ 再次发生碰撞
$\text{D.}$ $B$ 不能与 $A$ 再次发生碰撞
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
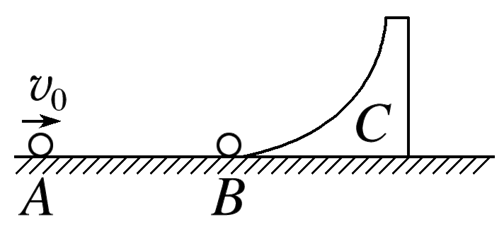
如图所示,一轻质弹簧的一端固定在滑块B上,另一端与滑块C接触但未连接,该整体静止放在离地面高为H=5 m的光滑水平桌面上.现有一滑块A从光滑曲面上离桌面高h=1.8 m处由静止开始滑下,与滑块B发生碰撞并粘在一起压缩弹簧推动滑块C向前运动,经过一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动,一段距离后从桌面边缘飞出.已知mA=1 kg,mB=2 kg,mC=3 kg,滑块A、B、C均可看作质点,取g=10 m/s2,不计空气阻力.求:
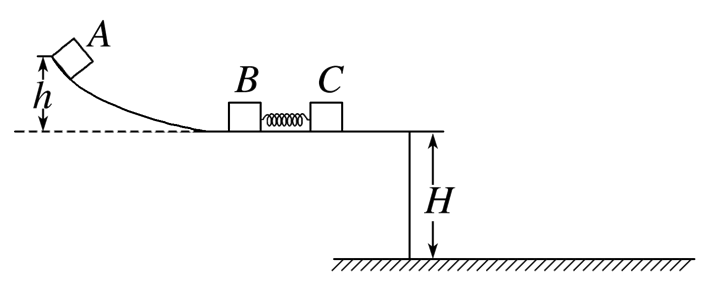
(1)滑块A与滑块B碰撞结束瞬间的速度大小;
(2)被压缩弹簧的最大弹性势能;
(3)滑块C落地点与桌面边缘的水平距离.