单选题 (共 10 题 ),每题只有一个选项正确
在万有引力定律的发现历程中,下列叙述符合史实的是
$\text{A.}$ 开普勒通过分析第谷的天文观测数据,发现了万有引力定律
$\text{B.}$ 丹麦天文学家第谷经过多年的天文观测和记录,提出了“日心说”的观点
$\text{C.}$ 卡文迪什通过实验推算出来引力常量G的值,被誉为第一个能“称量地球质量”的人
$\text{D.}$ 伽利略利用“地—月系统”验证了万有引力定律的正确性,使得万有引力定律得到了推广和更广泛的应用
火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知
$\text{A.}$ 太阳位于木星运行轨道的中心
$\text{B.}$ 火星和木星绕太阳运行速度的大小始终相等
$\text{C.}$ 火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方
$\text{D.}$ 相等时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
国际小行星中心于2021年10月8日确认公布了中国科学院紫金山天文台发现的一颗新彗星,命名为C/2021 S4.这颗彗星与太阳的最近距离约为7 AU,绕太阳转一圈约需要1 000年,假设地球绕太阳做圆周运动,地球与太阳的距离为1 AU,引力常量已知.则
$\text{A.}$ 由以上数据不可估算太阳的质量
$\text{B.}$ 由以上数据可估算太阳的密度
$\text{C.}$ 彗星由近日点向远日点运动时机械能增大
$\text{D.}$ 该彗星与太阳的最远距离约为193 AU
宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处.若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.已知该星球的半径与地球半径之比为R星∶R地=1∶4,地球表面重力加速度为g,设该星球表面附近的重力加速度大小为g′,空气阻力不计,忽略地球和星球自转的影响.则
$\text{A.}$ $g^{\prime}: g=1: 5$
$\text{B.}$ $g^{\prime}: g=5: 2$
$\text{C.}$ $M_{\text {星 }}: M_{\text {地 }}=1: 20$
$\text{D.}$ $M_{\text {星 }}: M_{\text {地 }}=1: 80$
国产科幻巨作《流浪地球》引起了人们对地球如何离开太阳系的热烈讨论.其中有一种思路是不断加速地球使其围绕太阳做半长轴逐渐增大的椭圆轨道运动,最终离开太阳系.假如其中某一过程地球刚好围绕太阳做椭圆轨道运动,地球到太阳的最近距离仍为R,最远距离为7R(R为加速前地球与太阳间的距离),则在该轨道上地球公转周期将变为
$\text{A.}$ 8年
$\text{B.}$ 6年
$\text{C.}$ 4年
$\text{D.}$ 2年
科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示.科学家认为S2的运动轨迹是半长轴约为1 000 AU(太阳到地球的距离为1 AU)的椭圆,银河系中心可能存在超大质量黑洞.这项研究工作获得了2020年诺贝尔物理学奖.若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为
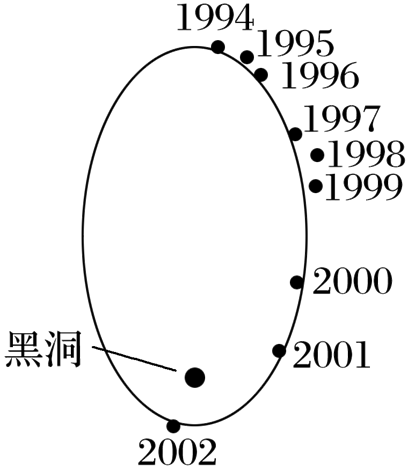
$\text{A.}$ $4 \times 10^4 M$
$\text{B.}$ $4 \times 10^6 M$
$\text{C.}$ $4 \times 10^8 M$
$\text{D.}$ $4 \times 10^{10} M$
8.将一质量为 $m$ 的物体分别放在地球的南,北两极点时,该物体的重力均为 $m g_0$ ;将该物体放在地球赤道上时,该物体的重力为 $m g$ .假设地球可视为质量均匀分布的球体,半径为 $R$ ,已知引力常量为 $G$ ,则由以上信息可得出
$\text{A.}$ $g_0$ 小于 $g$
$\text{B.}$ 地球的质量为 $\frac{g R^2}{G}$
$\text{C.}$ 地球自转的角速度为 $\omega=\sqrt{\frac{g_0-g}{R}}$
$\text{D.}$ 地球的平均密度为 $\frac{3 g}{4 \pi G R}$
2021年5月15日,"天问一号"着陆巡视器成功着陆于火星乌托邦平原,中国首次火星探测任务着陆火星取得圆满成功.如果着陆前着陆器近火星绕行的周期为 100 min .已知地球平均密度为 $5.5 \times$ $10^3 kg / m ^3$ ,地球近地卫星的周期为 85 min .估算火星的平均密度约为
$\text{A.}$ $3.8 \times 10^3 kg / m ^3$
$\text{B.}$ $4.0 \times 10^3 kg / m ^3$
$\text{C.}$ $4.2 \times 10^3 kg / m ^3$
$\text{D.}$ $4.5 \times 10^3 kg / m ^3$
如图所示,A、B两颗卫星绕地球做匀速圆周运动,O为地心,在两卫星运行过程中,AB连线和OA连线的夹角最大为θ,则A、B两卫星

$\text{A.}$ 做圆周运动的周期之比为 $2 \sqrt{\frac{1}{\sin ^3 \theta}}$
$\text{B.}$ 做圆周运动的周期之比为 $\frac{1}{\sin ^3 \theta}$
$\text{C.}$ 与地心 $O$ 连线在相等时间内扫过的面积之比为 $\sqrt{\frac{1}{\sin \theta}}$
$\text{D.}$ 与地心 $O$ 连线在相等时间内扫过的面积之比为 $\frac{1}{\sin \theta}$
若地球半径为 $R$ ,把地球看作质量分布均匀的球体."蛟龙号"下潜深度为 $d$ ,"天宫一号"轨道距离地面高度为 $h$ ,"蛟龙"号所在处与"天宫一号"所在处的重力加速度大小之比为(质量分布均匀的球壳对内部物体的万有引力为零)
$\text{A.}$ $\frac{R-d}{R+h}$
$\text{B.}$ $\frac{(R-d)^2}{(R+h)^2}$
$\text{C.}$ $\frac{(R-d)(R+h)^2}{R^3}$
$\text{D.}$ $\frac{(R-d)(R+h)}{R^2}$
多选题 (共 2 题 ),每题有多个选项正确
我国载人航天事业已迈入"空间站时代".若中国空间站绕地球近似做匀速圆周运动,运行周期为 $T$ ,轨道半径约为地球半径的 $\frac{17}{16}$ 倍,已知地球半径为 $R$ ,引力常量为 $G$ ,忽略地球自转的影响,则
$\text{A.}$ 漂浮在空间站中的宇航员不受地球的引力
$\text{B.}$ 空间站绕地球运动的线速度大小约为 $\frac{17 \pi R}{8 T}$
$\text{C.}$ 地球的平均密度约为 $\frac{3 \pi}{G T^2}\left(\frac{16}{17}\right)$ 3
$\text{D.}$ 空间站绕地球运动的向心加速度大小约为地面重力加速度的 $\left(\frac{16}{17}\right)^2$ 倍
两位科学家因为在银河系中心发现了一个超大质量的致密天体而获得了2020年诺贝尔物理学奖.他们对一颗靠近银河系中心的恒星S2的位置变化进行了持续观测,记录到的S2的椭圆轨道如图所示.图中O为椭圆的一个焦点,椭圆偏心率(离心率)约为0.87.P、Q分别为轨道的远银心点和近银心点,Q与O的距离约为120 AU(太阳到地球的距离为1 AU),S2的运行周期约为16年.假设S2的运动轨迹主要受银河系中心致密天体的万有引力影响,根据上述数据及日常的天文知识,可以推出

$\text{A.}$ S2与银河系中心致密天体的质量之比
$\text{B.}$ 银河系中心致密天体与太阳的质量之比
$\text{C.}$ S2在P点与Q点的速度大小之比
$\text{D.}$ S2在P点与Q点的加速度大小之比