单选题 (共 5 题 ),每题只有一个选项正确
一汽车通过拱形桥顶时速度为10 m/s,车对桥顶的压力为车重的 ,如果要使汽车在该桥顶对桥面恰好没有压力,车速为
$\text{A.}$ 15 m/s
$\text{B.}$ 20 m/s
$\text{C.}$ 25 m/s
$\text{D.}$ 30 m/s
如图所示,质量为 1.6 kg ,半径为 0.5 m 的光滑细圆管用轻杆固定在坚直平面内,小球 $A$ 和 $B$(均可视为质点)的直径略小于细圆管的内径(内径远小于细圆管半径).它们的质量分别为 $m_A=1 kg, ~ m_B=2 kg$ 。某时刻,小球 $A$ , $B$ 分别位于圆管最低点和最高点,且 $A$ 的速度大小为 $v_A=3 m / s$ ,此时杆对圆管的弹力为零.则 $B$ 球的速度大小 $v_B$ 为(取 $g=10 m / s ^2$ )

$\text{A.}$ $2 m / s$
$\text{B.}$ $4 m / s$
$\text{C.}$ $6 m / s$
$\text{D.}$ $8 m / s$
如图所示,叠放在水平转台上的物体 $A, ~ B$ 及物体 $C$ 能随转台一起以角速度 $\omega$ 匀速转动,$A, ~ B, ~ C$ 的质量分别为 $3 m, ~ 2 m, ~ m, ~ A$ 与 $B, ~ B$ 和 $C$ 与转台间的动摩擦因数都为 $\mu, ~ A$ 和 $B, ~ C$离转台中心的距离分别为 $r$ 和 $1.5 r$ 最大静摩擦力等于滑动摩擦力,物体 $A$ ,
$B, ~ C$ 均可视为质点,重力加速度为 $g$ ,下列说法正确的是
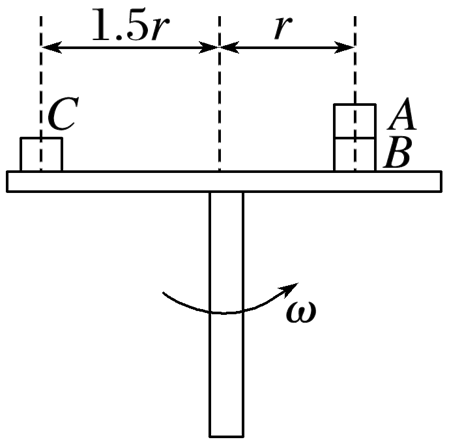
$\text{A.}$ $B$ 对 $A$ 的摩檫力一定为 $3 \mu m g$
$\text{B.}$ $B$ 对 $A$ 的摩擦力一定为 $3 m \omega^2 r$
$\text{C.}$ 转台的角速度需要满足 $\omega \leqslant \sqrt{\frac{\mu g}{r}}$
$\text{D.}$ 若转台的角速度逐渐增大,最先滑动的是 $A$ 物体
如图所示,轻杆长3L,在杆两端分别固定质量均为m的球A和B(均可视为质点),光滑水平转轴穿过杆上距球A为L处的O点,外界给系统一定能量后,杆和球在竖直平面内转动,球B运动到最高点时,杆对球B恰好无作用力.忽略空气阻力,重力加速度为g,则球B在最高点时
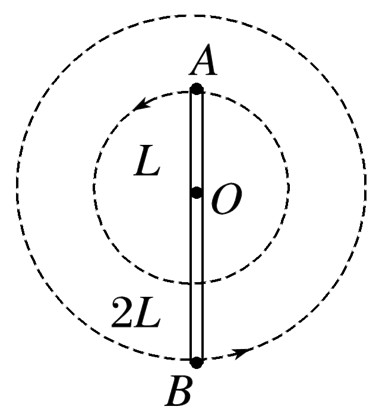
$\text{A.}$ 球B的速度为零
$\text{B.}$ 球A的速度大小为 $\sqrt{2gL}$
$\text{C.}$ 水平转轴对杆的作用力为1.5mg
$\text{D.}$ 水平转轴对杆的作用力为2.5mg
如图所示,在倾角为α=30°的光滑斜面上有一长L=0.8 m的轻杆,杆一端固定在O点,可绕O点自由转动,另一端系一质量为m=0.05 kg的小球(可视为质点),小球在斜面上做圆周运动,g取10 m/s2.要使小球能到达最高点A,则小球在最低点B的最小速度是
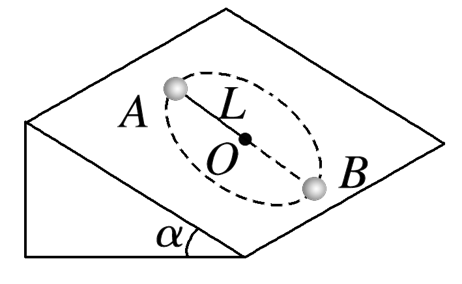
$\text{A.}$ $4 m / s$
$\text{B.}$ $2 \sqrt{10} m / s$
$\text{C.}$ $2 \sqrt{5} m / s$
$\text{D.}$ $2 \sqrt{2} m / s$
多选题 (共 5 题 ),每题有多个选项正确
如图所示,三角形为一光滑锥体的正视图,母线与竖直方向的夹角为θ=37°.一根长为l=1 m的细线一端系在锥体顶端,另一端系着一可视为质点的小球,小球在水平面内绕锥体的轴做匀速圆周运动,重力加速度g=10 m/s2,sin 37°=0.6,不计空气阻力,则
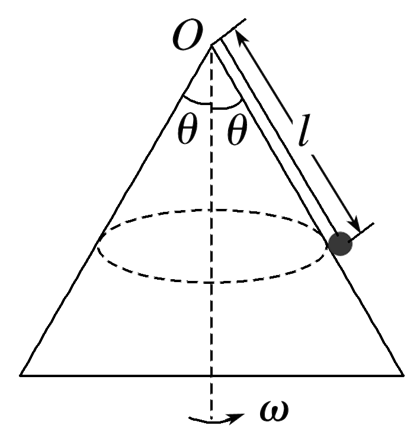
$\text{A.}$ 小球受重力,支持力,拉力和向心力
$\text{B.}$ 小球可能只受拉力和重力
$\text{C.}$ 当 $\omega=\frac{5}{2} \sqrt{2} rad / s$ 时,小球对锥体的压力刚好为零
$\text{D.}$ 当 $\omega=2 \sqrt{5} rad / s$ 时,小球受重力,支持力和拉力作用
如图所示,在竖直平面内有一半径为R的光滑固定细管(忽略管的内径),半径OB水平、OA竖直,一个直径略小于管内径的小球(可视为质点)由B点以某一初速度v0进入细管,之后从管内的A点以大小为vA的水平速度飞出.忽略空气阻力,重力加速度为g,

下列说法正确的是
$\text{A.}$ 为使小球能从 $A$ 点飞出,小球在 $B$ 点的初速度必须满足 $v_0>\sqrt{3 g R}$
$\text{B.}$ 为使小球能从 $A$ 点飞出,小球在 $B$ 点的初速度必须满足 $v_0>\sqrt{2 g R}$
$\text{C.}$ 为使小球从 $A$ 点水平飞出后再返回 $B$ 点,小球在 $B$ 点的初速度应为 $v_0$ $=\sqrt{\frac{5 g R}{2}}$
$\text{D.}$ 小球从 $A$ 点飞出的水平初速度必须满足 $v_A>\sqrt{g R}$ ,因而不可能使小球从 $A$ 点水平飞出后再返回 $B$ 点
如图所示,两个可视为质点的、相同的木块A和B放在转盘上,两者用长为L的水平细绳连接,木块与转盘间的最大静摩擦力均为各自重力的K倍,A放在距离转轴L处,整个装置能绕通过转盘中心的转轴O1O2转动,开始时,绳恰好伸直但无弹力,现让该装置从静止开始转动,使角速度缓慢增大,以下说法正确的是(重力加速度为g)
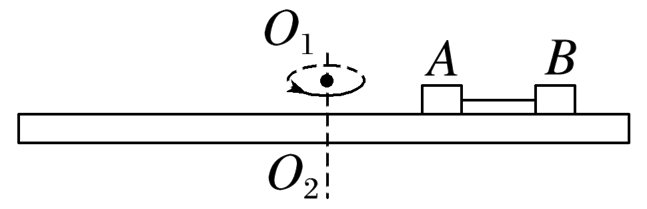
$\text{A.}$ 当 $\omega>\sqrt{\frac{2 K g}{3 L}}$ 时,$A, ~ B$ 会相对于转盘滑动
$\text{B.}$ 当 $\omega>\sqrt{\frac{K g}{2 L}}$ ,绳子一定有弹力
$\text{C.}$ $\omega$ 在 $\sqrt{\frac{K g}{2 L}} < \omega < \sqrt{\frac{2 K g}{3 L}}$ 范围内增大时,$B$ 所受摩擦力变大
$\text{D.}$ $\omega$ 在 $0 < \omega < \sqrt{\frac{2 K g}{3 L}}$ 范围内增大时,$A$ 所受摩擦力一直变大
如图甲所示的陀螺可在圆轨道的外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”,该玩具深受孩子们的喜爱.其物理原理可等效为如图乙所示的模型:半径为R的磁性圆轨道竖直固定,质量为m的小铁球(视为质点)在轨道外侧转动,A、B两点分别为轨道上的最高点、最低点.铁球受轨道的磁性引力始终指向圆心且大小不变,重力加速度为g,不计摩擦和空气阻力.

下列说法正确的是
$\text{A.}$ 铁球可能做匀速圆周运动
$\text{B.}$ 铁球绕轨道转动时机械能守恒
$\text{C.}$ 铁球在A点的速度一定大于或等于
$\text{D.}$ 要使铁球不脱轨,轨道对铁球的磁性引力至少为5mg
如图所示,竖直平面内有一半径为R=0.35 m且内壁光滑的圆形轨道,轨道底端与光滑水平面相切,一小球(可视为质点)以v0=3.5 m/s的初速度进入轨道,g=10 m/s2,则

$\text{A.}$ 小球不会脱离圆轨道
$\text{B.}$ 小球会脱离圆轨道
$\text{C.}$ 小球脱离轨道时的速度大小为
$\text{D.}$ 小球脱离轨道的位置与圆心连线和水平方向间的夹角为30°