单选题 (共 10 题 ),每题只有一个选项正确
设函数 $f(x)$ 在 $\mathbf{R}$ 上有定义, 且满足 $\lim _{x \rightarrow 0} \frac{f(x)-1}{x}=-1$, 则下列正确的是 ( )
$\text{A.}$ $f(0)=1$.
$\text{B.}$ $\lim _{x \rightarrow 0} f(x)=1$.
$\text{C.}$ $f^{\prime}(0)=-1$.
$\text{D.}$ $f^{\prime}(0)=1$.
设 $f(x)=\lim _{n \rightarrow \infty}(x-1) \arctan |x|^n$, 则
$\text{A.}$ $x=-1$ 为 $f(x)$ 的第一类间断点.
$\text{B.}$ $x=1$ 为 $f(x)$ 的第一类间断点.
$\text{C.}$ $x=-1$ 为 $f(x)$ 的第二类间断点.
$\text{D.}$ $x=1$ 为 $f(x)$ 的第二类间断点.
若 $\lim _{(x, y) \rightarrow(0,0)} \frac{f(x, y)-f(0,0)-x^3-2 y^3}{1-\cos \sqrt{x^2+y^2}}=2$, 则下列结论不正确的是
$\text{A.}$ $f(x, y)$ 在 $(0,0)$ 点连续.
$\text{B.}$ $f_x^{\prime}(0,0)=f_y^{\prime}(0,0)=0$.
$\text{C.}$ $f(x, y)$ 在 $(0,0)$ 处可微.
$\text{D.}$ $f(x, y)$ 在点 $(0,0)$ 处取极大值.
函数 $y=\frac{(x+1)^2}{x}$ 的图形有 $n$ 条渐近线, 则 $n=$ ( )
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设函数 $y=y(x)$ 由方程 $\ln \left(x^2+y^2\right)=\arctan \frac{y}{x}$ 确定, 且满足 $y(1)=0$, 则 $y^{\prime \prime}(1)=$ ( )
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{2}$.
$\text{C.}$ 10
$\text{D.}$ 20
已知函数 $f(x, y)=|x-y| g(x, y)$, 其中 $g(x, y)$ 在点 $(0,0)$ 的某邻域内有定义, 则 $f(x, y)$在点 $(0,0)$ 处偏导数存在的充分条件是
$\text{A.}$ $g(0,0)=0$.
$\text{B.}$ $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} g(x, y)$ 存在.
$\text{C.}$ $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} g(x, y)$ 存在且 $g(0,0)=0$.
$\text{D.}$ $g(x, y)$ 在点 $(0,0)$ 处连续, 且 $g(0,0)=0$.
设图数 $f(x, y)$ 在 $\mathbf{R}^{\circ}$ 上进续, 交抰祭次积分的顺序 $\int_{-2}^1 \mathrm{~d} x \int_{x^2}^{2-x} f(x, y) \mathrm{d} y=$
$\text{A.}$ $\int_1^4 \mathrm{~d} y \int_{\sqrt{y}}^{2-y} f(x, y) \mathrm{d} x$.
$\text{B.}$ $\int_1^4 \mathrm{~d} y \int_{2-y}^{\sqrt{y}} f(x, y) \mathrm{d} x$.
$\text{C.}$ $\int_0^1 \mathrm{~d} y \int_{\sqrt{y}}^{2-y} f(x, y) \mathrm{d} x+\int_1^4 \mathrm{~d} y \int_{2-y}^{\sqrt{y}} f(x, y) \mathrm{d} x$.
$\text{D.}$ $\int_0^1 \mathrm{~d} y \int_{\sqrt{y}}^{\sqrt{y}} f(x, y) \mathrm{d} x+\int_1^4 \mathrm{~d} y \int_{-\sqrt{y}}^{2-y} f(x, y) \mathrm{d} x$.
设 $|\boldsymbol{A}|=\left|\begin{array}{lll}1 & 1 & 1 \\ 1 & 2 & 0 \\ 1 & 0 & 3\end{array}\right|$, 则 $\sum_{i, j=1}^3 A_{i j}=$
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $\boldsymbol{A}$ 为 3 阶可逆矩阵,将 $\boldsymbol{A}$ 的第 1 行加到第 2 行得矩阵 $\boldsymbol{B}$, 再将矩阵 $\boldsymbol{B}$ 第 1 行乘 2 得矩阵 $\boldsymbol{C}$, 则 ${A C^{-1}}=$
$\text{A.}$ $\left[\begin{array}{ccc}\frac{1}{2} & 0 & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$.
$\text{B.}$ $\left[\begin{array}{ccc}\frac{1}{2} & 0 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$.
$\text{C.}$ $\left[\begin{array}{lll}2 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$.
$\text{D.}$ $\left[\begin{array}{lll}2 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$.
设 $\boldsymbol{A}, \boldsymbol{B}$ 均为 3 阶矩阵, 则必有
$\text{A.}$ $r(\boldsymbol{A}, \boldsymbol{A} \boldsymbol{B})=r(\boldsymbol{A})$.
$\text{B.}$ $r(\boldsymbol{A}, \boldsymbol{B A})=r(\boldsymbol{A})$.
$\text{C.}$ $r\left(\begin{array}{c}\boldsymbol{A} \\ \boldsymbol{A B}\end{array}\right)=r(\boldsymbol{A})$.
$\text{D.}$ $r(\boldsymbol{A B})=r(\boldsymbol{B A})$.
填空题 (共 6 题 ),请把答案直接填写在答题纸上
设 $f(x)=\int_1^x \frac{\ln (1+t)}{t} \mathrm{~d} t(x>0)$, 则 $f(2)+f\left(\frac{1}{2}\right)=$
$\lim _{n \rightarrow \infty} n\left[\mathrm{e}\left(1+\frac{1}{n}\right)^{-n}-1\right]=$
$\int_0^1 \ln (1+\sqrt{x}) \mathrm{d} x=$ ________ .
由曲线 $x y=3, x+y=4$ 围成的平面区域绕 $x$ 轴旋转一周所成旋转体体积为
设 $z=\sin x+\sin (x y)+\int_0^{x+y} \mathrm{e}^{t^2} \mathrm{~d} t$, 则 $\left.\mathrm{d} z\right|_{(0,0)}=$
设 3 阶矩阵 $\boldsymbol{A}$ 的第一行元素均为 1, 第一行元素的代数余子式为 1,2,3, 则方程组 $\boldsymbol{A x}=\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)$ 的解为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
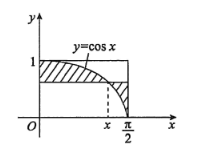
如图, 在 $\left(0, \frac{\pi}{2}\right)$ 内求一点 $x$, 使得阴影部分面积最小, 并求出该最小值.
设 $y=y(x)$ 为微分方程满足初值问题 $\left\{\begin{array}{l}\left(1-x^2\right) y^{\prime \prime}-x y^{\prime}=0, \\ y(0)=0, y^{\prime}(0)=1\end{array}\right.$ 的解, 求极限 $\lim _{x \rightarrow \frac{\sqrt{2}}{2}} \frac{y^2(x)-\frac{\pi^2}{16}}{2 x^2-1}$.
要制作一个中间为圆柱, 两端为相同的正圆雉的空浮标, 其体积为定值. 若要求用料最少, 求此时圆柱的高, 圆柱的半径和圆锥的高的比例.
求 $\iint_D|3 x+4 y| \mathrm{d} x \mathrm{~d} y$, 其中 $D=\left\{(x, y) \mid x^2+y^2 \leqslant 1\right\}$.
证明: 当 $x \geqslant 0$ 时, 存在 $\theta(x) \in(0,1)$, 使得 $\frac{\sqrt{x+1}+\sqrt{x}}{\sqrt{x+\theta(x)}}=2$, 且 $\theta(x)$ 满足:
( I ) $\frac{1}{4} \leqslant \theta(x) < \frac{1}{2} ;$
(II) $\lim _{x \rightarrow 0^{+}} \theta(x)=\frac{1}{4}, \lim _{x \rightarrow+\infty} \theta(x)=\frac{1}{2}$.
已知矩阵 $\boldsymbol{A}=\left[\begin{array}{ccc}4 & -3 & 1 \\ 2 & -1 & 1 \\ 0 & 0 & a\end{array}\right]$ 有二重特征值.
(I) 求 $a$ 的值;
(II) 矩阵 $\boldsymbol{A}$ 能否对角化? 若能, 求可逆矩阵 $\boldsymbol{P}$, 使得 $\boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P}$ 为对角矩阵.