单选题 （共 3 题 ），每题只有一个选项正确
三元一次方程组
$$
\left\{\begin{array}{l}
x_1+x_2+a x_3=4 \\
x_1-x_2+2 x_3=-4 \\
-x_1+a x_2+x_3=a^2
\end{array}\right.
$$
所代表的三平面不可能的位置关系为
$\text{A.}$ 
$\text{B.}$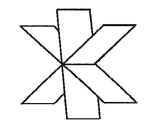 
$\text{C.}$ 
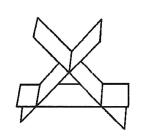$\text{D.}$ 
设 $n(n \geqslant 3)$ 阶矩阵
$$
A =\left(\begin{array}{ccccc}
1 & a & a & \cdots & a \\
a & 1 & a & \cdots & a \\
a & a & 1 & \cdots & a \\
\vdots & \vdots & \vdots & & \vdots \\
a & a & a & \cdots & 1
\end{array}\right),
$$
若矩阵 $A$ 的秩为 $n-1$, 则 $a$ 必为
$\text{A.}$ 1.
$\text{B.}$ $\frac{1}{1-n}$.
$\text{C.}$ -1 .
$\text{D.}$ $\frac{1}{n-1}$.
设二次型 $f\left(x_1, x_2, x_3\right)=a\left(x_1^2+x_2^2+x_3^2\right)+2 x_1 x_2+2 x_2 x_3+2 x_1 x_3$ 的正负惯性指数分别为 1,2 , 则
$\text{A.}$ $a>1$.
$\text{B.}$ $a < -2$.
$\text{C.}$ $-2 < a < 1$.
$\text{D.}$ $a=1$ 或 $a=-2$.