单选题 (共 8 题 ),每题只有一个选项正确
一弹簧振子,当把它水平放置时,它作简谐振动。若把它竖直放置或放在光滑斜面上,试判断下列情况正确的是
$\text{A.}$ 竖直放置作简谐振动,在光滑斜面上不作简谐振动;
$\text{B.}$ 竖直放置不作简谐振动,在光滑斜面上作简谐振动;
$\text{C.}$ 两种情况都作简谐振动
$\text{D.}$ 两种情况都不作简谐振动
两个简谐振动的振动曲线如图所示,则有
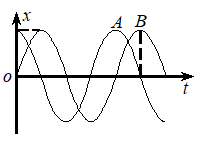
$\text{A.}$ $\mathrm{A}$ 超前 $\pi / 2$
$\text{B.}$ $\mathrm{A}$ 落后 $\pi / 2$
$\text{C.}$ $\mathrm{A}$ 超前 $\pi$
$\text{D.}$ $\mathrm{A}$ 落后 $\pi$ 。
一质点在 $x$ 轴上作简谐振动, 振辐 $A=4 \mathrm{~cm}$, 周期 $T=2 \mathrm{~s}$, 其平衡位置取作坐标原点. 若 $t$ $=0$ 时刻质点第一次通过 $x=-2 \mathrm{~cm}$ 处, 且向 $x$ 轴负方向运动, 则质点第二次通过 $x=-2 \mathrm{~cm}$ 处的时刻为
$\text{A.}$ $1 \mathrm{~s}$.
$\text{B.}$ $(2 / 3) \mathrm{s}$.
$\text{C.}$ $(4 / 3) \mathrm{s}$.
$\text{D.}$ $2 \mathrm{~s}$.
一个质点作简谐振动, 周期为 $\mathrm{T}$, 当质点由平衡位置向 $\mathrm{x}$ 轴正方向运动时, 由平衡位置到二分之一最大位移这段路程所需要的最短时间为
$\text{A.}$ $T / 4$
$\text{B.}$ $T / 12$
$\text{C.}$ $T / 6$
$\text{D.}$ $T / 8$
两个简谐振动的振动曲线如图所示, 若这两个简谐振动可叠加, 则合成的余弦振动的初相为:
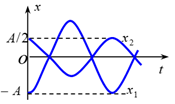
$\text{A.}$ $\pi / 2$
$\text{B.}$ $\pi$
$\text{C.}$ $-\pi / 2$
$\text{D.}$ 0
一质点作简谐振动. 其运动速度与时间的曲线如图所示. 若质点的振动规律用余弦函数描述,则其初相应为
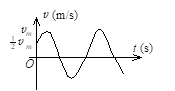
$\text{A.}$ $\pi / 6$.
$\text{B.}$ $5 \pi / 6$.
$\text{C.}$ $-5 \pi / 6$.
$\text{D.}$ $-\pi / 6$.
对一个作简谐振动的物体,下面哪种说法是正确的?
$\text{A.}$ 物体处在运动正方向的端点时,速度和加速度都达到最大值.
$\text{B.}$ 物体位于平衡位置且向负方向运动时,速度和加速度都为零.
$\text{C.}$ 物体位于平衡位置且向正方向运动时,速度最大,加速度为零.
$\text{D.}$ 物体处在负方向的端点时,速度最大,加速度为零.
一质点沿 $x$ 轴作简谐振动, 振动方程为 $x=4 \times 10^{-2} \cos \left(2 \pi t+\frac{1}{3} \pi\right)$ (SI)。从 $t=0$ 时刻起, 到质点位置在 $x=-2 \mathrm{~cm}$ 处, 且向 $x$ 轴正方向运动的最短时间间隔为
$\text{A.}$ $1 / 8 \mathrm{~s} $
$\text{B.}$ $1 / 4 \mathrm{~s}$.
$\text{C.}$ $1 / 2 \mathrm{~s}$
$\text{D.}$ $1 / 3 \mathrm{~s}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
一质点沿 $x$ 轴以 $x=0$ 为平衡位置作简谐振动. 频率为 $0.25 \mathrm{~Hz}, t=0$ 时, $x=-0.37 \mathrm{~cm}$ 而速度等于零, 则振幅是 ________ , 振动的数值表达式为 ________
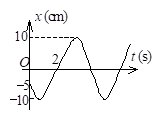
一简谐振动曲线如图所示, 则由图可确定在 $t=2 \mathrm{~s}$ 时刻质点的位移为 ________ , 速度为 ________

一简谐振子的振动曲线如图所示,则以余弦函数表示的振动方程为
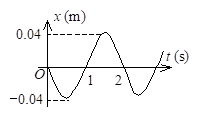
一质点作简谐振动. 其振动曲线如图所示. 根据此图, 它的周期 , 用余弦函数描述时初相
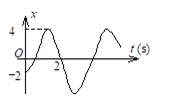
两个弹簧振子的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动,经过0.5s后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为
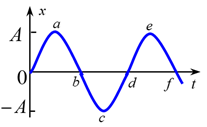
一水平弹簧简谐振子的振动曲线如图所示, 振子处在位移为零、速度为 ________ 、加速度为零和弹性力为零的状态, 对应于曲线上的 ________ 。振子处在位移的绝对值为 $A$ 、速度为零、加速度为 $-\omega^2 A$ 和弹性力 $\mathrm{kA}$ 的状态, 对应于曲线的 ________
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一质点作简谐振动, 其振动方程为 $x=0.24 \cos \left(\frac{1}{2} \pi t+\frac{1}{3} \pi\right)(\mathrm{SI})$, 试用旋转矢量法求出质点由初始状态 $(t=0$ 的状态) 运动到 $x=-0.12 \mathrm{~m}, v < 0$ 的状态所需最短时间 $\Delta t$ 。
一简谐振动的振动曲线如图所示. 求振动方程。
两个同方向简谐振动的振动方程分别为
$x_1=5 \times 10^{-2} \cos \left(10 t+\frac{3}{4} \pi\right)$(SI),
$x_2=6 \times 10^{-2} \cos \left(10 t+\frac{1}{4} \pi\right)$(SI),
求合振动方程.