单选题 (共 5 题 ),每题只有一个选项正确
一定量的理想气体, 分别经历如图(1)所示的 $a b c$ 过程, (图中虚线 $a c$ 为等温线), 和图(2)所示的 $d e f$ 过程(图中虚线 $d f$ 为 绝热线). 判断这两种过程是吸热还是放热.
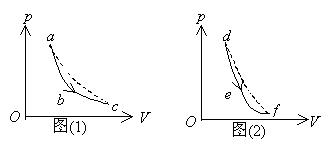
$\text{A.}$ $a b c$ 过程吸热, $d e f$ 过程放热.
$\text{B.}$ $a b c$ 过程放热, def 过程吸热.
$\text{C.}$ $a b c$ 过程和 $d e f$ 过程都吸热.
$\text{D.}$ $a b c$ 过程和 def 过程都放热.
质量一定的理想气体,从相同状态出发,分别经历等温过程、等压过程和绝热过程,使其体积增加一倍.那么气体温度的改变(绝对值)在
$\text{A.}$ 绝热过程中最大,等压过程中最小
$\text{B.}$ 绝热过程中最大,等温过程中最小
$\text{C.}$ 等压过程中最大,绝热过程中最小
$\text{D.}$ 等压过程中最大,等温过程中最小
一定量的理想气体经历 $a c b$ 过程时吸热 $500 \mathrm{~J}$. 则经历 $a c b d a$ 过程时, 吸热为
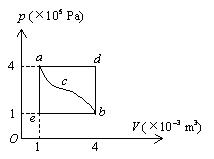
$\text{A.}$ $-1200 \mathrm{~J}$.
$\text{B.}$ $-700 \mathrm{~J}$.
$\text{C.}$ $-400 \mathrm{~J}$
$\text{D.}$ $700 \mathrm{~J}$
设高温热源的热力学温度是低温热源的热力学温度的n倍,则理想气体在一次卡诺循环中,传给低温热源的热量是从高温热源吸取热量的
$\text{A.}$ $n$ 倍.
$\text{B.}$ $n-1$ 倍 .
$\text{C.}$ $\frac{1}{n}$
$\text{D.}$ $\frac{n+1}{n}$倍 .
在温度分别为 $327^{\circ} \mathrm{C}$ 和 $27^{\circ} \mathrm{C}$ 的高温热源和低温热源之间工作的热机, 理论上的最大效率为
$\text{A.}$ $25 \%$
$\text{B.}$ $50 \%$
$\text{C.}$ $75 \%$
$\text{D.}$ $91.74 \%$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
一卡诺热机(可逆的), 低温热源的温度为 $27^{\circ} \mathrm{C}$ ,热机效率为 $40 \%$ ,其高温热源温度为 ________ K. 今欲将该热机效率提高 到 $50 \%$, 若低温热源保持不变, 则高温热源的温度应增加 ________ $\mathrm{K}$.
$1 \mathrm{~mol}$ 的单原子理想气体, 从状态 I $\left(p_1, V_1\right)$ 变化至状态 II $\left(p_2, V_2\right)$, 如图所示, 则此过程气体对外作的功为 ________ 吸收的热量 为 ________

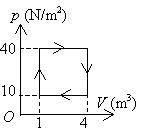
气体经历如图所示的一个循环过程,在这个循环中,外界传给气体的净热量是
一定量的理想气体,在 $p-T$ 图上经历一个如图所示的循环过程 $(a \rightarrow b \rightarrow c \rightarrow d \rightarrow a)$, 其中 $a \rightarrow b, c \rightarrow d$ 两个过程是绝热过 程, 则该循环的效率 $\eta=$
常温常压下, 一定量的某种理想气体(其分子可视为刚性分子, 自由度为 $i$ ), 在等压过程中吸热为 $Q$, 对外作功为 $W$, 内能增加为 $\Delta E$, 则 $W / Q=$ ________ , $\triangle E / Q=$ ________
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一定量的单原子分子理想气体, 从初态 $A$ 出发, 沿图示直线过程变到另一状态 $B$, 又经过等容、等压两过程回到状态 A.
(1)求 $A \rightarrow B, B \rightarrow C, C \rightarrow A$ 各过程中系统对外所作的功 $W$, 内能的增量 $\Delta E$ 以及所吸收的热量 $Q$.
(2)整个循环过程中系统对外所作的总功以及从外界吸收的总热量(过程吸热的代数和).

汽缸内有 $2 \mathrm{~mol}$ 氦气,初始温度为 $27^{\circ} \mathrm{C}$, 体积为 $20 \mathrm{~L}$ (升), 先将氦气等压膨胀,直至体积加倍,然后绝热膨涨,直至回 复初温为止. 把氦气视为理想气体. 试求:
(1)在 $p-V$ 图上大致画出气体的状态变化过程 .
(2)在这过程中氦气吸热多少?
(3)氦气的内能变化多少?
(4)氦气所作的总功是多少?
(普适气体常量 $R=8.31 \mathrm{~J} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}$ )
$1 \mathrm{~mol}$ 理想气体在 $T_1=400 \mathrm{~K}$ 的高温热源与 $T_2=300 \mathrm{~K}$ 的低温热源间作卡诺循环(可逆的),在 $400 \mathrm{~K}$ 的等温线上起始体 积为 $V_1=0.001 \mathrm{~m}^3$, 终止体积为 $V_2=0.005 \mathrm{~m}^3$, 试求此气体在每一循环中
(1) 从高温热源吸收的热量 $Q_1$
(2) 气体所作的净功 $W$
(3) 气体传给低温热源的热量 $Q_2$
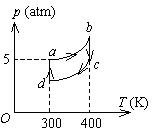
一定量的某种理想气体进行如图所示的循环过程. 已知气体在状态 $A$ 的温度为 $T_A=300 \mathrm{~K}$, 求
(1)气体在状态 $B 、 C$ 的温度;
(2)各过程中气体对外所作的功;
(3)经过整个循环过程, 气体从外界吸收的总热量(各过程吸热的代数和).

$0.02 \mathrm{~kg}$ 的氦气(视为理想气体), 温度由 $17^{\circ} \mathrm{C}$ 升为 $27^{\circ} \mathrm{C}$. 若在升温过程中, (1)体积保持不变; (2)压强保持不变; (3)不与 外界交换热量;试分别求出气体内能的改变、吸收的热量、外界对气体所作的功.(普适气体常量 $R=8.31 \mathrm{~J} \cdot \mathrm{mol}^{-1} \mathrm{~K}^{-1}$ )