单选题 (共 4 题 ),每题只有一个选项正确
若 $2 a-3 b=-1$ ,则代数式 $4 a^2-6 a b+3 b$ 的值为()
$\text{A.}$ -1
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
已知 $a, b$ 是方程 $x^2+x-3=0$ 的两个实数根,则 $a^2-b+2019$ 的值是
$\text{A.}$ 2023
$\text{B.}$ 2021
$\text{C.}$ 2020
$\text{D.}$ 2019
已知 $M, N$ 两点关于 $y$ 轴对称,且点 $M$ 在双曲线 $y=\frac{1}{2 x}$上,点 $N$ 在直线 $y=x+3$ 上,设点 $M$ 的坐标为 $(a, b)$ ,则二次函数 $y=-a b x^2+(a+b) x$
$\text{A.}$ 有最大值,最大值为 $\frac{9}{2}$
$\text{B.}$ 有最大值,最大值为 9
$\text{C.}$ 有最小值,最小值为 $\frac{9}{2}$
$\text{D.}$ 有最小值,最小值为 9
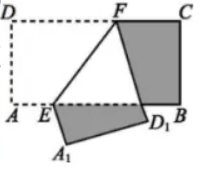
如图,在矩形 $A B C D_D$中,$A B=10, B C=5$ ,点 $E, F$ 分别在 $A B, C D$ 上,将矩形 $A B C D$ 沿 $E F$折叠,使点 $A, D$ 分别落在矩形 $A B C D$ 外部的点 $A_1, D_1$ 处,则阴影部分图形的周长为
$\text{A.}$ 15
$\text{B.}$ 20
$\text{C.}$ 25
$\text{D.}$ 30
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知 $x=2 y+3$ ,则代数式 $4 x-8 y+9$ 的值是
已知关于 $x$ 的一元二次方程 $(3 a-1) x^2-a x+\frac{1}{4}=0$ 有两个相等的实数根,则代数式 $a^2-2 a+1+\frac{1}{a}$ 的值等于
已知 $\left\{\begin{array}{l}x+2 y=4 k+1, \\ 2 x+y=k+2,\end{array}\right.$ 且 $0 < x+y < 3$ ,则 $k$ 的取值范围是
若 $x^2-3 x+1=0$ ,则 $\frac{x^2}{x^4+x^2+1}$ 的值为
已知 $(a+b)^2=7,(a-b)^2=3$ ,则 $a^2+b^2=$ , $\frac{1}{a^2+2}+\frac{1}{b^2+2}=$
若 $a-\frac{1}{a}=\sqrt{6}$ ,则 $a^2+\frac{1}{a^2}=$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
先化简,再求值:$(2 m+1)(2 m-1)-(m-1)^2+(2 m)^3 \div(-8 m)$ ,其中 $m$ 是方程 $x^2+x-2=0$ 的根.
阅 读 材 料:善 于 思 考 的 小 明在 解 方 程 组 $\left\{\begin{array}{l}4 x+10 y=6(1), \\ 8 x+22 y=10(2)\end{array}\right.$ 时,采用了一种"整体代换"的解法,解法如下:
解 :将 方 程 $8 x+20 y+2 y=10(2)$ ,变 形 为 $2(4 x+10 y)+2 y=10$(3),把方程(1)代入(3)得, $2 \times 6+2 y=10$ ,则 $y=-1$ ;把 $y=-1$ 代入(1)得,$x=4$ ,所以方程组的解为:$\left\{\begin{array}{l}x=4, \\ y=-1 .\end{array}\right.$
请你解决以下问题:
(1)试用小明的"整体代换"的方法解方程组 $\left\{\begin{array}{l}2 x-3 y=7(1), \\ 6 x-5 y=11(2) .\end{array}\right.$
(2)已知 $x, y, z$, 满足 $\left\{\begin{array}{l}3 x-2 z+12 y=47(1), \\ 2 x+z+8 y=36(2),\end{array}\right.$ 试求 $z$ 的值.