单选题 (共 6 题 ),每题只有一个选项正确
如图,图形甲与图形乙是位似图形,$O$ 是位似中心,位似比为$2:3$ ,点$A,B$ 的对应点分别为点$A',B'$, 若 $AB=6$,则 $A'B'$的长为 ( )

$\text{A.}$ $8$
$\text{B.}$ $9$
$\text{C.}$ $10$
$\text{D.}$ $15$
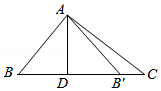
如图, 在 Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, \angle B=50^{\circ}, A D \perp B C$, 垂足为 $D, \triangle A D B$ 与 $\triangle A D B^{\prime}$ 关于直线 $A D$ 对称, 点 $B$ 的对称点是点 $B^{\prime}$, 则 $\angle C A B^{\prime}$ 的度数为 ( )
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $40^{\circ}$
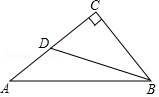
如图, Rt $\triangle A B C$ 中, $\angle C=90^{\circ}$, 点 $D$ 在 $A C$ 上, $\angle D B C=\angle A$. 若 $A C=4, \cos A=\frac{4}{5}$, 则 $B D$ 的长度为 ( )
$\text{A.}$ $\frac{9}{4}$
$\text{B.}$ $\frac{12}{5}$
$\text{C.}$ $\frac{15}{4}$
$\text{D.}$ $4$
如图, 面积为 1 的等边三角形 $A B C$ 中, $D, E, F$ 分别是 $A B, B C$, $C A$ 的中点, 则 $\triangle D E F$ 的面积是 ( )

$\text{A.}$ $1$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{4}$
如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于 ( )

$\text{A.}$ 10
$\text{B.}$ 5
$\text{C.}$ 4
$\text{D.}$ 3
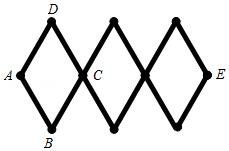
如图所示的木制活动衣帽架是由三个全等的菱形构成, 根据实际需 要可以调节 $A E$ 间的距离. 若 $A E$ 间的距离调节到 $60 \mathrm{~cm}$, 菱形的边长 $A B=20 \mathrm{~cm}$, 则 $\angle D A B$ 的度数是 ( )
$\text{A.}$ $90^{\circ}$
$\text{B.}$ $100^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $150^{\circ}$