设二维离散型随机变量 $(X, Y)$ 的概率分布为

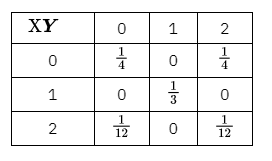
(1) 求 $P\{X=2 Y\}$ ；
(2) 求 $\operatorname{Cov}(X-Y, Y)$.

设随机变量 $\boldsymbol{X}$ 与 $Y$ 相互独立且分别服从正态分布 $N\left(\mu, \sigma^2\right)$ 与 $N\left(\mu, 2 \sigma^2\right)$ ，其中 $\sigma$ 是未知参数且 $\sigma>0$ ，设 $\boldsymbol{Z}=\boldsymbol{X}-\boldsymbol{Y}$ 。
(1) 求 $Z$ 的概率密度 $f\left(z ; \sigma^2\right)$ ；
(2) 设 $Z_1, Z_2, \cdots Z_n$ 为来自总体 $Z$ 的简单随机样本，求 $\sigma^2$ 的最大似然估计量 $\hat{\sigma}^2$ ；
(3) 证明 $\hat{\sigma}^2$ 为 $\sigma^2$ 的无偏估计量.