单选题 (共 6 题 ),每题只有一个选项正确
椭圆抛物面 $z=x^2+\frac{1}{4} y^2+3$ 到平面 $2 x-y+z=0$ 最近的点是?
$\text{A.}$ $(-1,2,5)$
$\text{B.}$ $(1,2,5)$
$\text{C.}$ $(1,-2,5)$
$\text{D.}$ $(-1,2,-5)$
函数 $z=x e^{2 y}$ 在点 $P(1,0)$ 处沿从 $P(1,0)$ 到 $Q(2,-1)$ 的方向导数是?
$\text{A.}$ $\frac{\sqrt{2}}{5}$
$\text{B.}$ $\frac{\sqrt{2}}{3}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $-\frac{\sqrt{2}}{2}$
过点 $(p, \sin p)$ 作曲线 $y=\sin x$ 的切线, 该曲线 (对应于 $0 \leqslant x \leqslant p$ 的部分) 与切线及 $y$ 轨所闹成平面图形的面积为 $S_1$, 与直线 $x=p$ 及 $x$ 轴所围成平面图形的面积为 $S_2$, 则 $\lim _{p-0} \frac{S_2}{S_1+S_2}=$
$\text{A.}$ $\frac{1}{3}$.
$\text{B.}$ $\frac{1}{2}$.
$\text{C.}$ $\frac{2}{3}$.
$\text{D.}$ 1
设 $\vec{T}^{\circ}=(\cos \alpha, \cos \beta)$ 是简单封闭曲线 $L$ 上点 $(x, y)$ 处指向逆时钟方向的单位切向量,则该点处指向曲线外侧的单位法向量 $\vec{n}^{\circ}=$
$\text{A.}$ $(-\cos \alpha,-\cos \beta)$
$\text{B.}$ $(\cos \beta, \cos \alpha)$
$\text{C.}$ $(\cos \beta,-\cos \alpha)$
$\text{D.}$ $(-\cos \beta, \cos \alpha)$
向量场 $\vec{u}(x, y, z)=x y^2 \vec{i}+y e^z \vec{j}+x \vec{k}$ 在点 $P(1,1,0)$ 处的旋度为
$\text{A.}$ $(1,1,2)$
$\text{B.}$ $(-1,-1,-2)$
$\text{C.}$ $2$
$\text{D.}$ $-2$
已知向量场 $\mathrm{F}(x, y)=(P(x, y), Q(x, y))$ ,如题图所示, $L$ 为圆周 $x^2+y^2=1$ ,且取逆时针方向,则曲线积分
$\oint_L P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y>0$ 所对应的向量场是
$\text{A.}$ 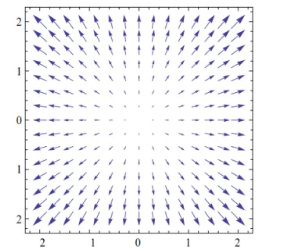 $\text{B.}$
$\text{B.}$ 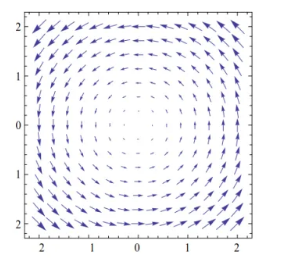 $\text{C.}$
$\text{C.}$ 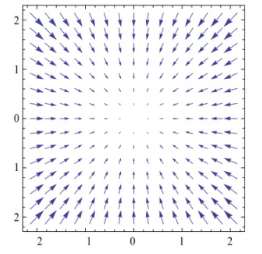 $\text{D.}$
$\text{D.}$