一、单选题 （共 3 题，每小题 5 分，共 50 分，每题只有一个选项正确）
若 $\frac{a^2}{a^2-2}=\frac{1}{1-\sqrt{2}-\sqrt{3}}$, 则 $\left(\frac{1}{1-a}-\frac{1}{1+a}\right) \div\left(\frac{a}{a^2-1}+a\right)$ 的值是
$\text{A.}$ $\sqrt{2}-\sqrt{3}$
$\text{B.}$ $\sqrt{3}-\sqrt{2}$
$\text{C.}$ $-\sqrt{2}-\sqrt{3}$
$\text{D.}$ $\sqrt{2}+\sqrt{3}$
如图, 平行四边形 $A B C D$ 中, $P$ 是四边形内任意一点, $\triangle A B P, \triangle B C P, \triangle C D P, \triangle A D P$的面积分别为 $S_1, S_2, S_3, S_4$, 则一定成立的是
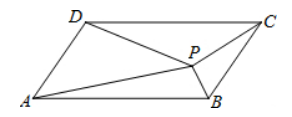
$\text{A.}$ $S_1+S_2=S_3+S_4$
$\text{B.}$ $S_1+S_2>S_3+S_4$
$\text{C.}$ $S_1+S_3=S_2+S_4$
$\text{D.}$ $S_1+S_2 < S_3+S_4$
如图, $\triangle A B P$ 为圆锥经过底面直径 $A B$ 的最大截面, $A B=6, P B=9$, 点 $C$ 为母线 $P B$ 的中点. 一只蜘蛛要从点 $A$ 沿圆雉侧面爬到点 $C$, 则该蜘蛛要爬的最短路径长为
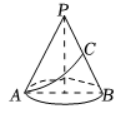
$\text{A.}$ 9
$\text{B.}$ $\frac{9}{2} \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $63 \sqrt{3}$
二、解答题 （ 共 6 题，满分 80 分，解答过程应写出必要的文字说明、证明过程或演算步骤 ）
若 $a b c=1$, 解方程 $\frac{2 a x}{a b+a+1}+\frac{2 b x}{b c+b+1}+\frac{2 c x}{c a+c+1}=1$
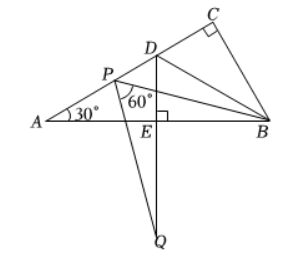
在Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, \angle A=30^{\circ}, B D$ 是 $\triangle A B C$ 的角平分线, $D E \perp A B$ 于点 $E$.在线段 $A D$ 上任取一点 $P$, 以 $P B$ 为一边, 在 $P B$ 的下方作 $\angle B P Q=60^{\circ}, P Q$ 交 $D E$ 延长线于点 $Q$. 请判断线段 $D A, D P, D Q$ 之间的数量关系, 并证明你的结论.
在曲线 $y=x^2(x \geq 0)$ 上点 $A$ 处作切线, 该切线与曲线以及 $x$ 轴所围图形的面积为 $\frac{1}{12}$.
(1) 求点 $A$ 的坐标和切线方程;
(2) 求由上述平面图形绕 $x$ 轴旋转一周所成旋转体的体积.
设 $a_1>0, a_{n+1}=a_n+\frac{1}{a_n}, n=1,2, \cdots$, 证明 $\lim _{n \rightarrow \infty} \frac{1}{a_n}=0$.
对函数 $y=\frac{x+1}{x^2}$ 填写下表:
证明当 $x>0$ 时, $\ln \left(x+\sqrt{1+x^2}\right) < \sqrt{1+x^2} \arctan x$.