解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
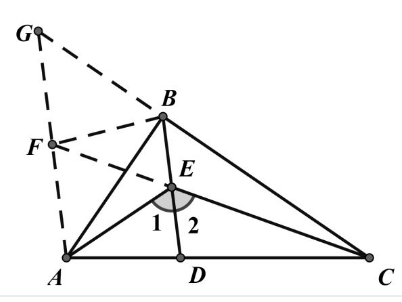
已知: 在 Rt $\triangle A B C$ 中, $\angle A B C=90^{\circ}, D$ 为 $A C$ 上一点, $E$ 是 $B D$ 的中点, $\angle 1=\angle 2$ 。 求证: $\angle A D B=2 \angle A B D$
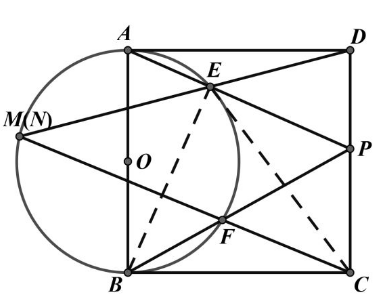
已知正方形 $A B C D, P$ 是 $C D$ 上的一点, 以 $A B$ 为直径的圆 $\odot O$ 交 $P A 、 P B$ 于 $E 、 F$, 射线 $D E 、 C F$ 交于点 $M$ 。求证:点 $M$ 在 $\odot O$ 上。
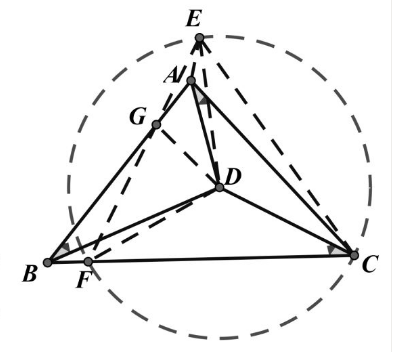
已知, 点 $D$ 是 $\triangle A B C$ 内一定点, 且有 $\angle D A C=\angle D C B=\angle D B A=30^{\circ}$ 。
求证: $\triangle A B C$ 是正三角形。
如图, 过正方形的顶点 $A$ 的直线交 $B C 、 C D$ 于 $M 、 N, D M$ 与 $B N$ 交于点 $L, B P \perp B N$, 交 $D M$ 于点 $P$ 。求证: (1) $C L \perp M N$; (2) $\angle M O N=\angle B P M$

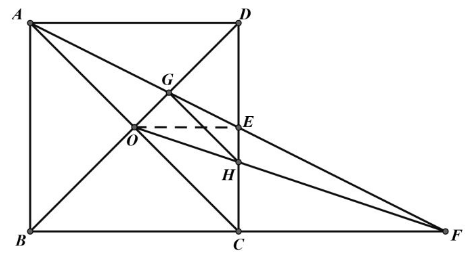
已知: 在正方形 $A B C D$ 中边长为 $1, E$ 是 $C D$ 上一点, $A E$ 交 $B D$ 于点 $G$, 交 $B C$ 的延长 线于点 $F$, 连接 $O F$, 交 $C D$ 于点 $H$, 连接 $G H$ 。
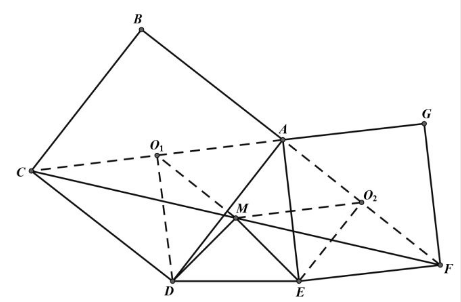
已知: $A B C D$ 与 $A E F G$ 均为正方形, 连接 $C F$, 取 $C F$ 的中点 $M$, 连接 $D M 、 M E$ 。
求证: $\triangle M D E$ 为等腰直角三角形