单选题 （共 11 题 ），每题只有一个选项正确
已知集合$M=\{x|-4 < x < 2\},N=\{x|x^2-x-6 < 0\}$ 则 $M \cap N=$ （ ）
$\text{A.}$ $\{x|-4 < x < 3 \}$
$\text{B.}$ $\{x|-4 < x < -2 \}$
$\text{C.}$ $\{x|-2 < x < 2 \} $
$\text{D.}$ $\{x|2 < x < 3 \}$
设复数 $z$ 满足$|z-i|=1$，$z$ 在复平面内对应的点为$(x，y)$，则 （ ）
$\text{A.}$ $(x+1)^2+y^2=1$
$\text{B.}$ $(x-1)^2+y^2=1$
$\text{C.}$ $x^2+(y-1)^2=1$
$\text{D.}$ $x^2+(y+1)^2=1$
已知$a=log_2 0.2, b=2^{0.2} , c=0.2^{0.3}$,则 （ ）
$\text{A.}$ $a < b < c$
$\text{B.}$ $a < c < b$
$\text{C.}$ $c < a < b$
$\text{D.}$ $b < c < a$
古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是
$\dfrac{\sqrt5 -1}{2}$
（$\dfrac{\sqrt5 -1}{2} ≈0.618$ 称为黄金分割比例)，
著名的“断臂维纳斯”便是如此．
此外，最美人体的头顶至咽喉的长度与咽喉
至肚脐的长度之比也是$\dfrac{\sqrt5 -1}{2}$,
若某人满足上述两个黄金分割比例，
且腿长为 105 cm，头顶至脖子
下端的长度为 26 cm，则其身高可能是 （ ）
$\text{A.}$ $165cm$
$\text{B.}$ $175cm$
$\text{C.}$ $185cm$
$\text{D.}$ $190cm$
函数$f(x)=\dfrac{sin x+x}{cos x+x^2}$ 在$[-\pi,\pi]$的图像大致为
$\text{A.}$ 
$\text{B.}$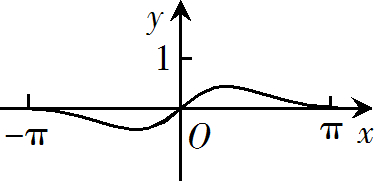 
$\text{C.}$ 
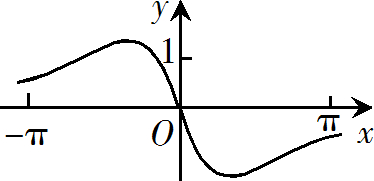$\text{D.}$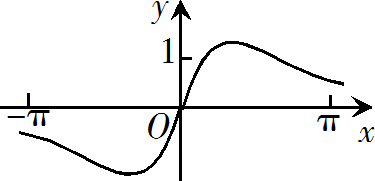 
我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的 6 个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有 3 个阳爻的概率是 （ ）
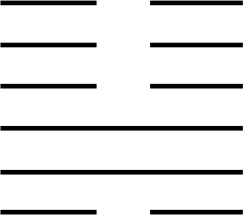
$\text{A.}$ $5 \over 16$
$\text{B.}$ $11 \over 32$
$\text{C.}$ $21 \over 32$
$\text{D.}$ $11 \over 16$
如图是求 $ \frac{1}{2+\frac{1}{2+\frac{1}{2}}} $ 的程序框图, 图中空白框中应填入 （ ）
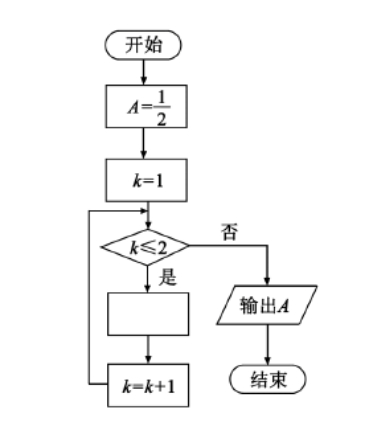
$\text{A.}$ $A=\frac{1}{2+A}$
$\text{B.}$ $A=2+\frac{1}{A}$
$\text{C.}$ $A=\frac{1}{1+2 A}$
$\text{D.}$ $A=1+\frac{1}{2 A}$
记 $S_{n}$ 为等差数列$ \{a_{n}\} $ 的前$n$项和. 已知 $ S_{4}=0, a_{5}=5 $ 则 （ ）
$\text{A.}$ $a_n=2n-5$
$\text{B.}$ $a_n=3n-10$
$\text{C.}$ $S_n=2n^2-8n$
$\text{D.}$ $S_n=\dfrac{1}{2}n^2-2n$
已知椭圆的焦点为 $ F_{1}(-1,0)$,$ F_{2}(1,0)$ , 过$F_{2}$ 的直线与 C 交于 A, B 两点. 若 $\left|A F_{2}\right|=2\left|F_{2} B\right| $ ,$|AB|=|BF_1|$, 则C的方程为 （ ）
$\text{A.}$ $\frac{x^{2}}{2}+y^{2}=1$
$\text{B.}$ $\frac{x^{2}}{3}+\frac{y^{2}}{2}=1$
$\text{C.}$ $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$
$\text{D.}$ $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$
关于函数$f(x)=\sin |x|+|\sin x|$有下述四个结论
1.$f(x)$是偶函数
2.$f(x)$在区间 $\left(\frac{\pi}{2}, \pi\right)$ 单调递增
3.$f(x)$在$[-\pi,\pi]$有4个零点。
4.$(f(x)$的最大值为2
其中所有正确的结论编号是
$\text{A.}$ $(1) (2) (4)$
$\text{B.}$ $((2) (4)$
$\text{C.}$ $(1) (4)$
$\text{D.}$ $(1) (3) $
已知三棱锥 P−ABC 的四个顶点在球 O 的球面上，PA=PB=PC，△ABC 是边长为 2 的正三角形，E，F 分别是 PA，AB 的中点，∠CEF=90°，则球 O 的体积为
$\text{A.}$ $8 \sqrt{6} \pi$
$\text{B.}$ $4 \sqrt{6} \pi$
$\text{C.}$ $2 \sqrt{6} \pi$
$\text{D.}$ $ \sqrt{6} \pi$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
曲线$y=3\left(x^{2}+x\right) \mathrm{e}^{x}$ 在点$(0,0)$处的切线方程为
记$S_n$为等比数列$\{a_n\}$的前$n$项和，若 $a_1=\dfrac{1}{3}, a_4^2=a_6$,则 $S_5=$
甲、乙两队进行篮球决赛，采取七场四胜制（当一队赢得四场胜利时，该队获胜，决赛结束）．根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”．设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4∶1获胜的概率是
已知双曲线$C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若 $\overrightarrow{F_{1} A}=\overrightarrow{A B}, \quad \overrightarrow{F_{1} B} \cdot \overrightarrow{F_{2} B}=0 $，则C的离心率为
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知非零向量 $ {a}, {b} $ 满足 $|{a}|=2|{b}|$ , 且 $({a}-{b}) \perp {b} $ , 则$ {a} $ 与 $ {b} $ 的夹角为 （ ）
$ \triangle A B C $ 的内角 $ A, B, C $ 的对边分别为 $ a, b, c$ , 设 $ (\sin B-\sin C)^{2}=\sin ^{2} A-\sin B \sin C $.
(1) 求 $ A$;
(2) 若 $\sqrt{2} a+b=2 c $, 求$ \sin C$
如图，直四棱柱$ ABCD–A_1B_1C_1D_1 $的底面是菱形， $AA_1=4 ， AB=2 ， ∠ BAD=60°， E， M， N $ 分别是
$BC，BB_1，A_1D$ 的中点．
(1)证明：$MN$∥平面 $C_1DE$；
(2)求二面角 $A−MA_1−N$ 的正弦值
已知抛物线$C：y^2=3x$ 的焦点为F，斜率为$\dfrac{3}{2}$的直线l与C的交点为A，B，与x轴的交点为P．
（1）若$|AF|+|BF|=4$，求 $l$ 的方程；
（2）若$\overrightarrow{A P}=3 \overrightarrow{P B}$ ，求$|AB|$．
已知函数$f(x)=\sin x-\ln (1+x)$，$f'(x)$为$f(x)$的导数．证明：
（1）$f'(x)$在区间$(-1,\dfrac{-\pi}{2})$存在唯一极大值点；
（2）$f(x)$有且仅有2个零点．
为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X．
（1）求的分布列；
（2）若甲药、乙药在试验开始时都赋予4分，$p_{i}(i=0,1, \cdots, 8)$表示“甲药的累计得分为$i$时，最终认为甲药比乙药更有效”的概率，则 $p_{0}=0, \quad p_{8}=1, \quad p_{i}=a p_{i-1}+b p_{i}+c p_{i+1}(i=1,2, \cdots, 7)$, 其中 $a=P(X=-1), b=P(X=0),c=P(X=1)$
假设 $\alpha=0.5, \beta=0.8$
(i)证明： $ \left\{p_{i+1}-p_{i}\right\}(i=0,1,2, \cdots, 7) $ 为等比数列；
(ii)求$P_4$，并根据$P_4$的值解释这种试验方案的合理性．
在直角坐标系$xOy$中，曲线C的参数方程为 $\left\{\begin{array}{l}
x=\frac{1-t^{2}}{1+t^{2}} \\
y=\frac{4 t}{1+t^{2}}
\end{array}\right.$（t为参数）．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为．$2 \rho \cos \theta+\sqrt{3} \rho \sin \theta+11=0$
（1）求C和l的直角坐标方程；
（2）求C上的点到l距离的最小值．
已知$a，b，c$为正数，且满足$abc=1$．证明：
（1）$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leq a^{2}+b^{2}+c^{2}$
（2）$(a+b)^{3}+(b+c)^{3}+(c+a)^{3} \geq 24$