单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \mid x^{2} \leq 1\right\}, B=\{y \mid y \geq-1\}$, 则 $A \cap B=$()
$\text{A.}$ $\varnothing$
$\text{B.}$ $[-1,1]$
$\text{C.}$ $\lfloor-1,+\infty)$
$\text{D.}$ $[-1,1)$
设 $m \in \mathbf{R}$, 若复数 $z_{1}=-2+\mathrm{i}$ 的虚部与复数 $z_{2}=m+m \mathrm{i}$ 的虚部相等, 则 $z_{1} \cdot z_{2}=($ )
$\text{A.}$ $-3+\mathrm{i}$
$\text{B.}$ $-1-\mathrm{i}$
$\text{C.}$ $3-\mathrm{i}$
$\text{D.}$ $-3-\mathrm{i}$
已知向量 $\vec{a}, \vec{b}$, 的夹角为 $\frac{\pi}{3}$, 且 $|\vec{a}|=2,|\vec{b}|=3$, 则 $\vec{a} \cdot(\vec{b}-\vec{a})=($ )
$\text{A.}$ $-1$
$\text{B.}$ $3 \sqrt{3}-4$
$\text{C.}$ $-2$
$\text{D.}$ 1
某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团, 该校共有 2000 名同学, 每名同学依据自己 的兴趣爱好最多可参加其中一个, 各个社团的人数比例的饼状图如图所示, 其中参加朗诵社团的同学有 8 名, 参加太极拳社团的有 12 名, 则()

$\text{A.}$ 这五个社团的总人数为 100
$\text{B.}$ 脱口秀社团的人数占五个社团总人数的 $20 \%$
$\text{C.}$ 这五个社团总人数占该校学生人数的 $8 \%$
$\text{D.}$ 从这五个社团中任选一人, 其来脱口秀社团或舞蹈社团的概率为 $50 \%$
执行如图所示的程序框图,输出的 s 值为 ( )
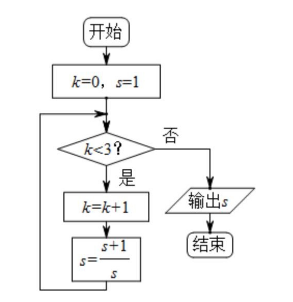
$\text{A.}$ 2
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{5}{3}$
$\text{D.}$ $\frac{8}{5}$
若 $a=\lg 0.3, b=\log _{3} 2, c=\log _{5} 4$, 则()
$\text{A.}$ $c>b>a$
$\text{B.}$ $b>c>a$
$\text{C.}$ $c>a>b$
$\text{D.}$ $a>b>c$
若 $\sin (\pi-\alpha)=\frac{4}{5}$, 则 $\cos 2 \alpha=$
$\text{A.}$ $-\frac{24}{25}$
$\text{B.}$ $\frac{7}{25}$
$\text{C.}$ $-\frac{7}{25}$
$\text{D.}$ $\frac{24}{25}$
设变量 $x, y$ 满足约束条件 $\left\{\begin{array}{c}x+y-2 \leq 0 \\ x-y+2 \geq 0 \\ x \geq-1 \\ y \geq-1\end{array}\right.$, 则目标函数 $z=x+y$ 的最小值为 ( )
$\text{A.}$ 2
$\text{B.}$ $-3$
$\text{C.}$ $-2$
$\text{D.}$ 0
已知直线 $y=k x(k>0)$ 与圆 $C:(x-2)^{2}+(y-1)^{2}=4$ 相交于 $A, B$ 两点 $|A B|=2 \sqrt{3}$, 则 $k=($ )
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{4}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{5}{12}$
若直线 $x=\frac{\pi}{4}$ 是曲线 $y=\sin \left(\omega x-\frac{\pi}{4}\right)(\omega>0)$ 的一条对称轴, 且函数 $y=\sin \left(\omega x-\frac{\pi}{4}\right)$ 在区间 $\left[0, \frac{\pi}{12}\right]$ 上不单调, 则 $\omega$ 的最小值为()
$\text{A.}$ 9
$\text{B.}$ 7
$\text{C.}$ 11
$\text{D.}$ 3
已知 $f(x-1)$ 是定义为 $\mathrm{R}$ 上的奇函数, $f(1)=0$, 且 $f(x)$ 在 $[-1,0)$ 上单调递增, 在 $[0,+\infty)$ 上单调递减, 则不等式 $f\left(2^{x}-3\right) < 0$ 的解集为()
$\text{A.}$ $(1,2)$
$\text{B.}$ $(-\infty, 1)$
$\text{C.}$ $(2,+\infty)$
$\text{D.}$ $(-\infty, 1) \cup(2,+\infty)$
如图 1 所示, 双曲线具有光学性质; 从双曲线右焦点发出的光线经过双曲线镜面反射, 其反射光线的反 向延长线经过双曲线的左焦点. 若双曲线 $E: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左、右焦点分别为 $F_{1}, F_{2}$, 从 $F_{2}$ 发 出的光线经过图 2 中的 $A, B$ 两点反射后, 分别经过点 $C$ 和 $D$, 且 $\cos \angle B A C=-\frac{3}{5}, A B \perp B D$, 则 $E$ 的 离心率为()
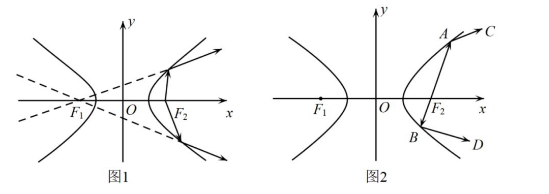
$\text{A.}$ $\frac{\sqrt{5}}{2}$
$\text{B.}$ $\frac{\sqrt{17}}{3}$
$\text{C.}$ $\frac{\sqrt{10}}{2}$
$\text{D.}$ $\sqrt{5}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
记等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 若 $a_{3}=0, a_{4}+a_{5}=3$, 则 $S_{11}=$
若函数 $f(x)=x \ln x+1$, 则 $f(x)$ 在点 $(1, f(1))$ 处的切线方程为
已知 $F_{1}, F_{2}$ 是椭圆 $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$ 的左、右焦点, $P$ 在椭圆上运动, 求 $\frac{1}{\left|P F_{1}\right|}+\frac{1}{\left|P F_{2}\right|}$ 的最小值为
在正方体 $A B C D-A_{1} B_{1} C_{1} D_{1}$ 中, 点 $E$ 为线段 $B_{1} D_{1}$ 上的动点, 现有下面四个命题:
(1)直线 $D E$ 与直线 $A C$ 所成角为定值; (2) 点 $E$ 到直线 $A B$ 的距离为定值;
(3)三棱雉 $E-A_{1} B D$ 的体积为定值; (4)三棱雉 $E-A_{1} B D$ 外接球的体积为定值.
其中所有真命题的序号是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在锐角 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 所对的边分别为 $a 、 b 、 c$, 已知 $2 a \sin C=\sqrt{3} c$.
(1) 求角 $A$ 的大小;
(2) 若 $b=2, a=\sqrt{7}$, 求 $\triangle A B C$ 的面积.
已知数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=1, a_{n+1}=2 a_{n}+1$.
(1) 证明 $\left\{a_{n}+1\right\}$ 是等比数列, 并求 $\left\{a_{n}\right\}$ 的通项公式;
(2) 求数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和公式.
2022 年北京冬奥会的申办成功与“ 3 亿人上冰雪”口号的提出, 将冰雪这个冷项目迅速炒“热”. 北京某综 合大学计划在一年级开设冰球课程, 为了解学生对冰球运动的兴趣, 随机从该校一年级学生中抽取了 200 人进行调查, 其中女生中对冰球运动有兴趣的占 $\frac{2}{3}$, 而男生有 20 人表示对冰球运动没有兴趣.
(1)完成 $2 \times 2$ 列联表, 并回答能否有 $97.5 \%$ 的把握认为“对冰球是否有兴趣与性别有关”?
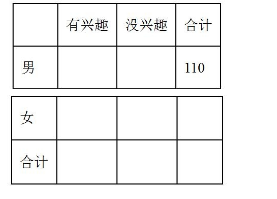
(2)已知在被调查的女生中有 5 名数学系的学生, 其中 3 名对冰球有兴趣, 现在从这 5 名学生中随机抽取 2 人, 求至少有 1 人对冰球有兴趣的概率.
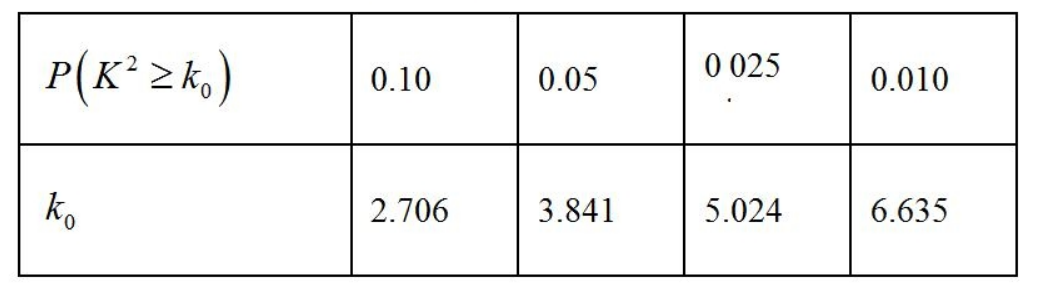
$$K^{2}=\frac{n(a d-b c)^{2}}{(a+b)(c+d)(a+c)(b+d)}$$
如图, 在三棱锥 $P-A B C$ 中, $A B=B C=2, P A=P B=P C=A C=2 \sqrt{2}, O$ 为 $A C$ 的中点.

(1) 证明: $P O \perp$ 平面 $A B C$;
(2) 若点 $M$ 在棱 $B C$ 上, 且 $M C=2 M B$, 求点 $C$ 到平面 $P O M$ 的距离.
已知函数 $f(x)=\ln x+\frac{a}{x}-2 x$.
(1)讨论当 $a>0$ 时, $f(x)$ 单调性.
证明: $\mathrm{e}^{x}+\frac{a-2 x^{2}-2 x}{x}>f(x)$.
已知平面上动点 $Q(x, y)$ 到 $F(0,1)$ 的距离比 $Q(x, y)$ 到直线 $l: y=-2$ 的距离小 1 , 记动点 $Q(x$,
y) 的轨迹为曲线 $C$.
(1) 求曲线 $C$ 的方程.
(2)设点 $P$ 的坐标为 $(0,-1)$, 过点 $P$ 作曲线 $C$ 的切线, 切点为 $A$, 若过点 $P$ 的直线 $m$ 与曲线 $C$ 交于 $M$, $N$ 两点, 证明: $\angle A F M=\angle A F N$.