一、单选题 (共 12 题 ),每题只有一个选项正确
1. 化简 的结果是
2. 下列运算正确的是
3. 一个数是,这个数用科学记数法表示为
4. 下列说法正确的是
两点之间,直线最短;
过一点有一条直线平行于已知直线;
和已知直线垂直的直线有且只有一条;
在平面内过一点有且只有一条直线垂直于已知直线.
5. 如果一个角的补角是,那么这个角的余角的度数是
6. 如图,下列条件中,能判定
的是
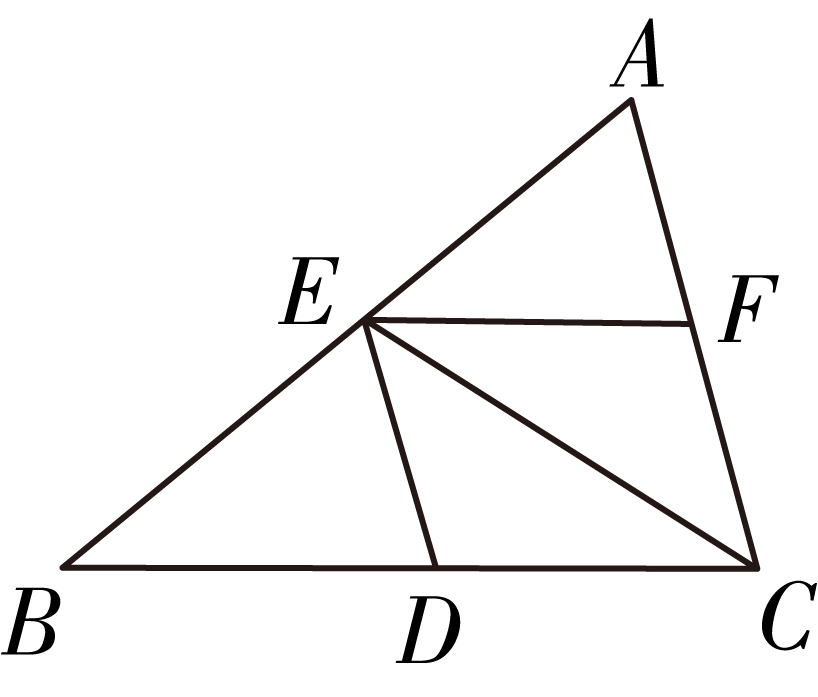
7. 下列各式中不能用平方差公式进行计算的是
8. 若,那么的值是
9. 下列计算中,正确的是
10. 若,,则等于
5
3
15
10
11. 若是一个完全平方式,则的值是
12. 通过下图面积的计算,验证一个恒等式,此等式是

二、填空题 (共 6 题 ),请把答案直接填写在答题纸上
14. 计算: ________ .
15. 在下列说法中①同位角相等;②对顶角相等; ③等角的补角相等; ④两直线平行,同旁内角相等.正确的说法有 ________ (写编号)
16. 计算: ________ .
17. 若,且,则 ________ .
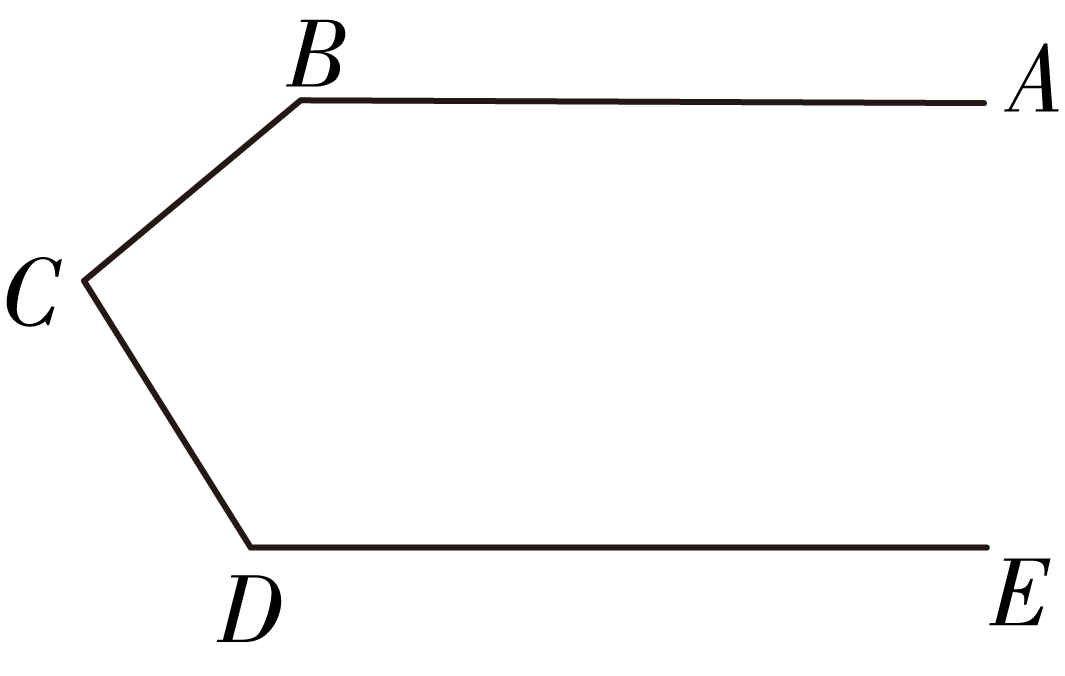
18. 如图,
,
,
,则
的度数是 ________ .
三、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
19. 解答题.
(1) 计算:
(2)
(3)
(4)
(5)
20. 解答题.
(1)
(2)
(3)
(4)
21. 先化简,后求值.
,其中,
22. 如图,某市有一块长为(
)米,宽为(
)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
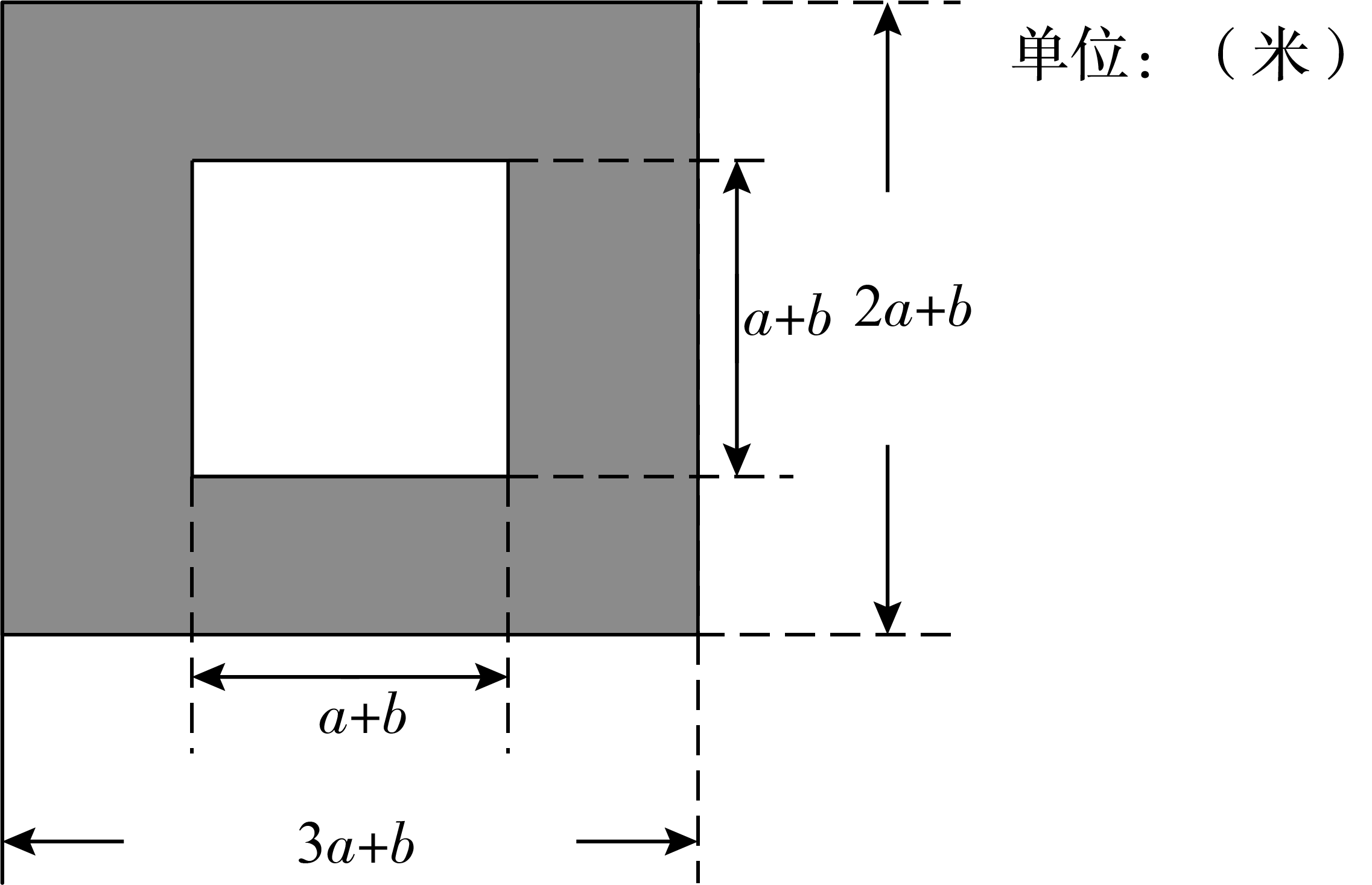
(1)绿化的面积是多少平方米?
(2) 求出当
, 时的绿化面积.
23. 如图,已知
,
,证明
.

证明:
, ________
________
________ , ________
,(两直线平行,内错角相等)
,
________ ,
________ .
24. 观察下列各式.
(1) 根据以上规律: 则
(2) 你能由此推出一般规律:
(3)根据以上规律: 的值.