2023年浙江省绍兴市中考模拟数学试卷（含答案）

导出试卷

2023年浙江省绍兴市中考模拟数学试卷（含答案）

一、单选题（共 10 题），每题只有一个选项正确

1. 在

0, 2, - 3, - \frac{1}{2}

这四个数中, 最小的数是

A.

B.

C.

-3

D.

- \frac{1}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 去年某城镇人均可支配收入为 34181 元, 34181 用科学记数法可表示为

a \times 10^{4}

, 则

a

的值是

A.

0.34181

B.

3.4181

C.

D.

0.3

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

3. 已知一个几何体如图所示, 则该几何体的左视图是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 某路口红绿灯的时间设置如下: 绿灯 60 秒, 红灯 40 秒, 黄灯 3 秒, 当车随机经过该路口, 遇到哪一种灯的可能性最大

A.

绿灯

B.

红灯

C.

黄灯

D.

不能确定

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 下列计算正确的是

A.

a^{3} + a^{2} = a^{5}

B.

(3 a - b)^{2} = 9 a^{2} - b^{2}

C.

{(- a b^{3})}^{2} = a^{2} b^{6}

D.

a^{6} b + a^{2} = a^{3} b

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 若一个

n

边形的内角和为

900^{\circ}

, 则

n

的值是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 二次函数

y = a x^{2} + b x + c

自变量

x

与函数值

y

的对应关系如下表, 设一元二次方程

a x^{2} + b x + c = 0

的根为

x_{1}, x_{2}

, 且

x_{1} < x_{2}

, 则下列说法正确的是

A.

- 1.5 < x_{1} < - 1

B.

- 1 < x_{1} < - 0.5

C.

0.5 < x_{2} < 1

D.

1 < x_{2} < 1.5

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 如图,

E

是正方形

A B C D

内一点,

A E ⊥ D E

于

E, A E = 2 cm

, 则

△ A B E

的面积是( )

{cm}^{2}

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 如图, 在平面直角坐标系中, 已知

A (- 3, - 2), B (0, - 2), C (- 3, 0), M

是线段

A B

上的
一个动点, 连接

C M

, 过点

M

作

M N ⊥ M C

交

y

轴于点

N

. 若点

M, N

在直线

y = k x + b

上, 则

b

的最大值是

A.

- \frac{7}{8}

B.

- \frac{3}{4}

C.

- 1

D.

- \frac{7}{4}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 如图, 在菱形

A B C D

中, 对角线

A C 、 B D

交于点

O

, 以

A C

为斜边作

R t △ A E C, A E

与

B D

交于点

F

, 连接

B E

, 使得

B F = C O

, 且

∠ E B F = 2 ∠ C A E

, 若

A C = 2

, 则菱形

A B C D

的周长为

A.

4 \sqrt{6}

B.

4 \sqrt{3}

C.

4 \sqrt{2}

D.

4

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 6 题），请把答案直接填写在答题纸上

11. 若

\frac{2 x}{x + 1}

有意义, 则

x

的取值范围是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 已知

{\begin{cases} x = 1 \\ y = - 1 \end{cases}

是方程

3 x - a y = 5

的一个解, 那么

a

的值是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 中国古代最初用“三分损益法”确定宫、啇、角、徵、羽五声音阶，例如：假设能发出第一个基准音的乐器的长度为 81 , 那么能发出第二个基准音的乐器的长度为

81 \times (1 - \frac{1}{3}) = 54

, 能发出第三个基准音的乐器的长度为

54 \times (1 + \frac{1}{3}) = 72 \dots

(也就是依次先减少三分之一, 后增加三分之一). 假设能发出第一个基准音的乐哭的长度为

a

, 能发出第四个基准音的乐器的长度是 32 , 则

a

的值是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 将两个直角三角尺按如图所示方式摆放, 点

A 、 D

分别在边

E F 、 B C

上,

∠ B A C = ∠ E D F = 90^{\circ}, ∠ E = 45^{\circ}, ∠ C = 30^{\circ}, A B

与

D F

交于点

M

, 若

B C / / E F

, 则

∠ B M D

的大小为（　　）度.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 如图, 点

A, C

为函数

y = \frac{k}{x} (x < 0)

图象上的两点, 过

A, C

分别作

A B ⊥ x

轴,

C D ⊥ x

轴, 丢足分别为

B, D

, 连接

O A, A C, O C

, 线段

O C

交

A B

于点

E

, 且点

E

恰好为

O C

的中点. 当

△ A E C

的面积为

\frac{3}{4}

时,

k

的值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 如图, 矩形纸片

A B C D, A D = 12, A B = 4

, 点

E

在线段

B C

上, 将

△ E C D

沿

D E

向上翻折, 点

C

的对应点

C^{'}

落在线段

A D

上, 点

M, N

分别是线段

A D

与线段

B C

上的点，将四边形

A B N M

沿

M N

向上翻折, 点

B

恰好落在线段

D E

的中点

B^{'}

处, 则线段

M N

的长

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 8 题），解答过程应写出必要的文字说明、证明过程或演算步骤

17. （1）计算:

{(\frac{1}{2})}^{- 1} + \sqrt{12} - 4 \sin 60^{\circ}

;
（2）解方程:

2 x^{2} + 3 x - 3 = 0

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 某校为了促进学生的个性发展, 计划开设四类拓展性课程, 包括艺术体育类、自然科学类、人文社科类及其他晃 (每人唯选一项, 要求人人都要參加). 为了解学生喜爱哪种课程, 学校做了一次抽样调查. 根据收集到的数据, 绘制成如下两幅不完整的统计图.

请根据图中的信息回答下列问题:
(1)此次抽样调査的样本容量是（　　）人;
(2)求人文社科类在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生, 请估计喜欢艺术体育类拓展课的学生人数.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 在平面直角坐标系中, 若两点的横坐标不相等, 纵坐标互为相反数, 则称这两点关于

x

轴斜对称. 其中一点叫做另一点关于

x

轴的斜对称点. 如: 点

(- 4, 2), (1, - 2)

关于

x

轴斜对称，在平面直角坐标系

x O y

中，点

A

的坐标为

(2, 1)

(1)下列各点中, 与点

A

关于

x

轴斜对称的是 (只㙋序号);
①

(3, - 1)

, ②

(- 2, 1)

, ③

(2, - 1)

, ④

(- 1, - 1)

.
(2) 若点

A

关于

x

轴的斜对称点

B

恰好落在直线

y = k x + 3 k + 1

上,

△ A O B

的面积为 3 , 求

k

的值；
(3)抛物线

y = x^{2} - b x - 1

上恰有两个点

M 、 N

与点

A

关于

x

轴斜对称, 抛物线的顶点为

D

, 且

V D M N

为等腰直角三角形, 则

b

的值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 在某两个时刻, 太阳光线与地面的夹角分别为

37^{\circ}

和

45^{\circ}

, 树

A B

长

6 m

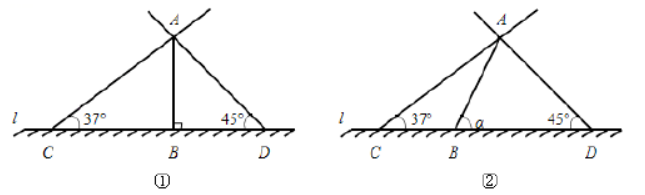
(1)如图①, 若树与地面

l

的夹角为

90^{\circ}

, 则两次影长的和

C D =

m;
(2)如图②, 若树与地面

l

的夹角为

α

, 求两次影长的和

C D

(用含

α

的式子表示).
(参考数据:

\sin 37^{\circ} \approx 0.60, \cos 37^{\circ} \approx 0.80, \tan 37^{\circ} \approx 0.75

)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 如图,

A, B, C

是

O

上的三点, 且

A B = 2 B C

. 过点

B

作

B E ⊥ O C

于点

E

, 延长

B O

交

O

于点

D

, 连结

A D

.
(1) 若

∠ A D B = 62^{\circ}

, 求

∠ O B E

的度数;
(2)求证:

A B = 2 B E

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22. 如图, 在平行四边形

A B C D

中, 对角线

A C 、 B D

相交于点

O, B D = 2 B C, E 、 F

、

G

分别是

O C 、 O D 、 A B

的中点.

(1)求证

B E ⊥ A C

;
(2)连接

A F

, 求证: 四边形

A G E F

是棱形。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 如图, 在平面直角坐标系

x O y

中, 攵物线

y = x^{2} + a x + a - 5

与

x

轴交于点

A, B

两点 (点

A

在点

B

的左则), 与

y

轴交于点

C

, 对称轴是直线

x = - 1

(1)求抛物线的解析式及顶点坐标;
(2)若

P (n, c)

和

Q (2, b)

是抛物线上两点, 且

c < b

, 求

n

的取值范围;

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

24. 如图, 在

◻ A B C D

中,

∠ A D B = 90^{\circ}, A B = 10 cm, A D = 8 cm

, 点

P

从点

D

出发, 沿

D A

方向匀速运动. 速度为

2 cm / s

; 同时, 点

Q

从点

B

出发, 沿

B C

方向匀速运动, 速度为

1 cm / s

. 当一个点停止迫动, 另一个点也停止运动. 过点

P

作

P E / / B D

交

A B

于点

E

, 连接

P Q

, 交

B D

于点

F

. 设适动时间为

t (s) (0 < t < 4)

. 解答下列问题:

(1)当

t

为何值时,

P Q / / A B

?
(2) 连接

E Q

, 设四边形

A P Q E

的面积为

y ({cm}^{2})

, 求

y

与

t

的函数关系式.
(3)若点

F

关于

A B

的对称点为

F^{'}

, 是否存在某一时刻

t

, 使得点

P, E, F

三点共线? 若存在, 求出

t

的值; 若不存在, 请说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。