单选题 (共 9 题 ),每题只有一个选项正确
如图,用两根等长的细绳将一匀质圆柱体悬挂在坚直木板的 $P$ 点,将木板以底边 $M N$ 为轴向后方缓慢转动直至水平,绳与木板之间的夹角保持不变,忽略圆柱体与木板之间的摩擦,在转动过程中
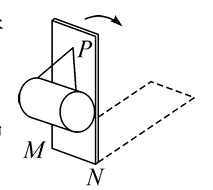
$\text{A.}$ 圆柱体对木板的压力逐渐增大
$\text{B.}$ 圆柱体对木板的压力先增大后减小
$\text{C.}$ 两根细绳上的拉力均先增大后减小
$\text{D.}$ 两根细绳对圆柱体拉力的合力保持不变
质量为 $M$ 的凹槽静止在水平地面上,内壁为半圆柱面,截面如图所示,$A$ 为半圆的最低点,$B$ 为半圆水平直径的端点。凹槽恰好与坚直墙面接触,内有一质量为 $m$ 的小滑块。
用推力 $F$ 推动小滑块由 $A$ 点向 $B$ 点缓慢移动,力 $F$ 的方向始终沿圆弧的切线方向,在此过程中所有摩擦均叮忽略,下列说法正确的是
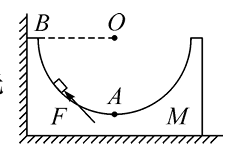
$\text{A.}$ 推力 $F$ 先增大后减小
$\text{B.}$ 凹槽对滑块的支持力先减小后增大
$\text{C.}$ 墙面对凹槽的压力先增大后减小
$\text{D.}$ 水平地面对凹槽的支持力先减小后增大
如图所示为一简易起重装置,(不计一切阻力)$A C$ 是上端带有滑轮的固定支架,$B C$为质量不计的轻杆,杆的一端 $C$ 用铰链固定在支架上,另一端 $B$ 悬挂一个质量为 $m$ 的重物,并用钢丝绳跨过滑轮 $A$ 连接在卷扬机上。开始时,杆 $B C$ 与 $A C$ 的夹角 $\angle B C A>90^{\circ}$ ,现使 $\angle B C A$缓缓变小,直到 $\angle B C A=30^{\circ}$ 。在此过程中,杆 $B C$ 所产生的弹力
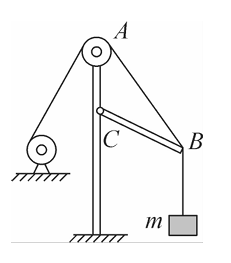
$\text{A.}$ 大小不变
$\text{B.}$ 逐渐增大
$\text{C.}$ 先增大后减小
$\text{D.}$ 先减小后增大
如图,柔软轻绳 $O N$ 的一端 $O$ 固定,其中间某点 $M$ 拴一重物,用手拉住绳的另一端 $N$ 。初始时,$O M$ 坚直且 $M N$ 被拉直,$O M$ 与 $M N$ 之间的夹角为 $\alpha\left(\alpha>\frac{\pi}{2}\right)$ 。现将重物向右上方缓慢拉起,并保持夹角 $\alpha$ 不变。在 OM 由坚直被拉到水平的过程中
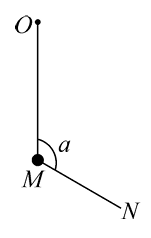
$\text{A.}$ $M N$ 上的张力逐渐增大
$\text{B.}$ $M N$ 上的张力先增大后减小
$\text{C.}$ $O M$ 上的张力逐渐增大
$\text{D.}$ $O M$ 上的张力先增大后减小
如图所示,在坚直放置的穹形支架上,一根长度不变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物 $G$ 。现将轻绳的一端固定于支架上的 $A$ 点,另一端从 $B$ 点沿支架缓慢地向 $C$点靠近( $C$ 点与 $A$ 点等高)。则在此过程中绳中拉力大小
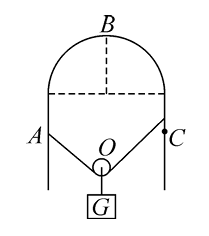
$\text{A.}$ 先变大后不变
$\text{B.}$ 先变大后变小
$\text{C.}$ 先变小后不变
$\text{D.}$ 先变小后变大
课堂上,老师准备了"$\llcorner$"形光滑木板和三个完全相同、外表面光滑的匀质圆柱形积木,要将三个积木按图所示(截面图)方式堆放在木板上,则木板与水平面夹角 $\theta$ 的最大值为
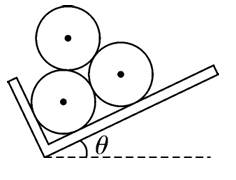
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
如图所示,一轻质光滑定滑轮固定在倾斜木板上,质量分别为 $m$ 和 $2 m$ 的物块 $A$ 、
$B$ ,通过不可伸长的轻绳跨过滑轮连接,$A 、 B$间的接触面和轻绳均与木板平行。 $A$ 与 $B$间、 $B$ 与木板间的动摩擦因数均为 $\mu$ ,设最大静摩擦力等于滑动摩擦力。当木板与水平面的夹角为 $45^{\circ}$ 时,物块 $A 、 B$ 刚好要滑动,则 $\mu$的值为
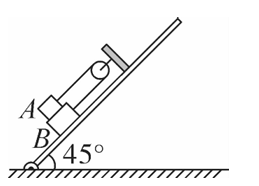
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{1}{6}$
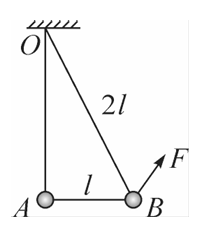
如图所示,重力都为 $G$ 的两个小球 $A$ 和 $B$ 用三段轻绳连接后悬挂在 $O$ 点上,$O 、 B$ 间的绳子长度是 $2 l, A 、 B$ 间的绳子长度是
$l$ 。将一个拉力 $F$ 作用到小球 $B$ 上,使三段轻绳都伸直,同时 $O 、 A$ 间和 $A 、 B$ 间的两段轻绳分别处于坚直和水平方向上,则拉力 $F$ 的最小值为
$\text{A.}$ $\frac{1}{2} G$
$\text{B.}$ $\frac{\sqrt{3}}{3} G$
$\text{C.}$ $G$
$\text{D.}$ $\frac{2 \sqrt{3}}{3} G$
如图所示,学校门口水平地面上有一质量为 m 的石墩,石墩与水平地面间的动摩擦因数为 $\mu$ ,工作人员用轻绳按图示方式匀速移动石墩时,两平行轻绳与水平面间的夹角均为$\theta$ ,则下列说法正确的是

$\text{A.}$ 轻绳的合拉力大小为 $\mu m g$
$\text{B.}$ 轻绳的合拉力大小为 $\frac{\mu m g}{\cos \theta+\mu \sin \theta}$
$\text{C.}$ 减小夹角 $\theta$ ,轻绳的合拉力一定减小
$\text{D.}$ 轻绳的合拉力最小时,地面对石墩的摩擦力也最小
多选题 (共 7 题 ),每题有多个选项正确
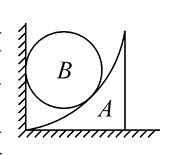
如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体 $A, A$ 的左端紧靠坚直墙,$A$ 与坚直墙之间放一光滑圆球 $B$ ,已知 $A$的圆半径为球 $B$ 的半径的 3 倍,球 $B$ 所受的重力为 $G$ ,整个装置处于静止状态。设墙壁对 $B$ 的支持力为 $F_1, A$ 对 $B$ 的支持力为 $F_2$ ,若把 $A$ 向右移动少许后,它们仍处于静止状态,则 $F_1 、 F_2$ 的变化情况分别是
$\text{A.}$ $F_1$ 减小
$\text{B.}$ $F_1$ 增大
$\text{C.}$ $F_2$ 增大
$\text{D.}$ $F_2$ 减小
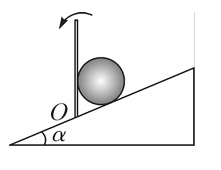
如图所示,在倾角为 $\alpha$ 的斜面上,放一质量为 $m$ 的小球,小球和斜坡及挡板间均无摩擦,当挡板绕 $O$ 点逆时针缓慢地转向水平位置的过程中,则有
$\text{A.}$ 斜面对球的支持力逐渐增大
$\text{B.}$ 斜面对球的支持力逐渐减小
$\text{C.}$ 挡板对小球的弹力先减小后增大
$\text{D.}$ 挡板对小球的弹力先增大后减小
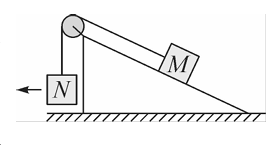
如图,一粗糙斜面固定在地面上,斜面顶端装有一光滑定滑轮,一细绳跨过滑轮,其一端悬挂物块 $N$ 。另一端与斜面上的物块 $M$ 相连,系统处于静止状态。现用水平向左的拉力缓慢拉动 $N$ ,直至悬挂 $N$ 的细绳与坚直方向成 $45^{\circ}$ 。已知 $M$ 始终保持静止,则在此过程中
$\text{A.}$ 水平拉力的大小可能保持不变
$\text{B.}$ $M$ 所受细绳的拉力大小一定一直增加
$\text{C.}$ $M$ 所受斜面的摩擦力大小一定一直增加
$\text{D.}$ $M$ 所受斜面的摩擦力大小可能先减小后增加
如图所示,某工厂将圆柱形工件 $a$ 放在倾角为 $\theta$ 的斜面上,为防止工件滚动,在其下方垫一段半径与 $a$ 相同的半圆柱体 $b$ ,若逐渐减小斜面倾角,$a 、 b$ 始终处于静止状态,不计 $a$与接触面的摩擦,$b$ 的质量很小。则( )
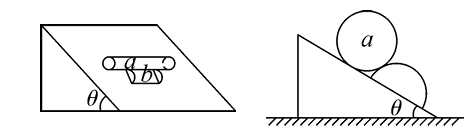
$\text{A.}$ 斜面对 $a$ 的弹力变大
$\text{B.}$ 斜面对 $a$ 的弹力先变大后变小
$\text{C.}$ $b$ 对 $a$ 的弹力逐渐变小
$\text{D.}$ $b$ 对 $a$ 的弹力不变
如图所示,倾角为 $\alpha$ 的粗糙斜劈放在粗糙水平面上,物体 $a$ 放在斜面上,轻质细线一端固定在物体 $a$ 上,另一端绕过光滑的滑轮固定在 $c$ 点,滑轮2下悬挂物体 $b$ ,系统处于静止状态。若将固定点 $c$ 向右移动少许,而 $a$ 与斜劈始终静止,则
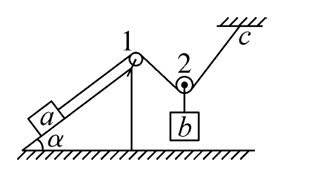
$\text{A.}$ 细线对物体 $a$ 的拉力增大
$\text{B.}$ 斜劈对地面的压力减小
$\text{C.}$ 斜劈对物体 $a$ 的摩擦力减小
$\text{D.}$ 地面对斜劈的摩擦力增大
如图,表面粗糙的楔形物块 $A$ 静置在水平地面上,斜面上有小物块 $B$ ,用平行于斜面的力 $F$ 拉 $B$ ,使之沿斜面匀速上滑。现逆时针缓慢旋转该力至图中虚线位置,并保证在旋转该力过程中物块 $B$ 一直处于匀速上滑状态,且在 $B$ 运动的过程中,楔形物块 $A$ 始终保持静止。则在力 $F$ 旋转的过程中,下列关于各力变化的说法正确的是
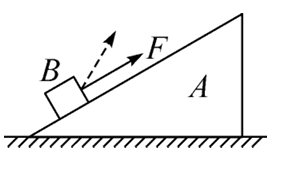
$\text{A.}$ $F$ 可能一直减小
$\text{B.}$ 物块 B 受到的摩擦力可能不变
$\text{C.}$ 物块的对斜面的作用力一定减小
$\text{D.}$ 地面受到的摩擦力大小可能不变
《大国工匠》节目中讲述了王进利用"秋千法"在 1000 kV 的高压线上带电作业的过程,如图所示,绝缘轻绳 $O D$ 一端固定在高压线杆塔上的 $O$ 点,另一端固定在兜篮上。另一绝缘轻绳跨过固定在杆塔上 $C$ 点的定滑轮,一端连接兜篮,另一端由工人控制。身穿屏蔽服的王进坐在兜篮里,缓慢地从 $C$ 点运动到处于 $O$ 点正下方 $E$ 点的电缆处。绳 $O D$一直处于伸直状态,兜篮、王进及携带的设备总质量为 $m$ ,不计一切阻力,重力加速度大小为 $g$ 。关于王进从 $C$ 点运动到 $E$ 点的过程中,下列说法正确的是
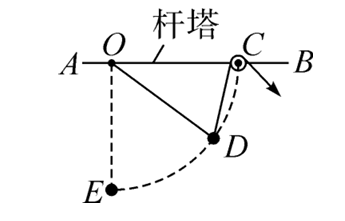
$\text{A.}$ 工人对绳的拉力一直变大
$\text{B.}$ 绳 $O D$ 的拉力的一直变小
$\text{C.}$ $O D 、 C D$ 两绳拉力的合力大小等于 $m g$
$\text{D.}$ 当绳 $C D$ 与坚直方向的夹角为 $30^{\circ}$ 时,工人对绳的拉力为 $\frac{\sqrt{3}}{3} m g$
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
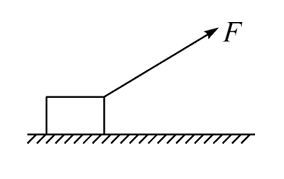
如图所示,质量 $m=5.2 \mathrm{~kg}$ 的金属块放在水平地面上,在斜向上的拉力 $F$ 作用下,向右以 $v_0=2.0 \mathrm{~m} / \mathrm{s}$ 的速度做匀速直线运动。已知金属块与地面间的动摩擦因数 $\mu=0.2$ , $g=10 \mathrm{~m} / \mathrm{s}^2$ ,求所需拉力 $F$ 的最小值。