单选题 (共 5 题 ),每题只有一个选项正确
实数 $a$ 在数轴上的位置如图所示,则化简 $\sqrt{a^2-8 a+16}+\sqrt{(a-11)^2}$ 结果为

$\text{A.}$ 7
$\text{B.}$ -7
$\text{C.}$ $2 a-15$
$\text{D.}$ 无法确定
实数 $a, b$ 在数轴上的位置如图所示,则 $\sqrt{a^2}-\sqrt{b^2}-|a-b|$ 化简的结果是
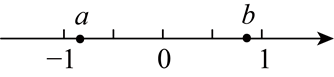
$\text{A.}$ $-2 b$
$\text{B.}$ $-2 a$
$\text{C.}$ $2 b-2 a$
$\text{D.}$ 0
若 $\sqrt{2} \leq a \leq \sqrt{3}$ ,则化简 $\sqrt{a^2-2 a+1}-|a-2|$ 的结果是
$\text{A.}$ $2 a-3$
$\text{B.}$ -1
$\text{C.}$ $-a$
$\text{D.}$ 1
已知 $b < a < 0$ ,那么 $|a-b|+\sqrt{(a+b)^2}$ 的结果是
$\text{A.}$ $-2 b$
$\text{B.}$ $2 b$
$\text{C.}$ $-2 a$
$\text{D.}$ $2 a$
已知点 $P(a, b)$ 是平面直角坐标系中第二象限的点,则化简 $\sqrt{a^2}-\sqrt{b^2}-(\sqrt{b-a})^2$ 的结果是
$\text{A.}$ $-2 b$
$\text{B.}$ $-2 a$
$\text{C.}$ $2(b-a)$
$\text{D.}$ 0
填空题 (共 3 题 ),请把答案直接填写在答题纸上
当 $x>1$ 时,化简 $\sqrt{\frac{2 x^2}{1-2 x+x^2}}$ 的结果是
已知三角形 $ A B C$ 的三边之长分别为 $2 、 5 、 m$ ,则 $\sqrt{(m-3)^2}-\sqrt{m^2-14 m+49}=$
已知 $0 < a < 1$ ,则 $\sqrt{a^2+\frac{1}{a^2}-2} \div\left(1-\frac{1}{a}\right)=$
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求代数式 $a+\sqrt{1-2 a+a^2}$ 的值,其中 $a=1007$ ,如图是小亮和小芳的解答过程:
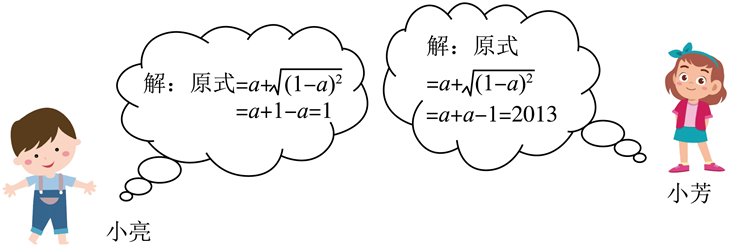
(1) $\_\_\_\_$的解法是错误的;
(2)求代数式 $a+2 \sqrt{a^2-6 a+9}$ 的值,其中 $a=-2024$ .
【阅读理解】
在解决数学问题时,我们一般先仔细阅读题干,找出有用信息作为已知条件,然后利用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件;而有的信息不太明显,需要结合图形、特殊式子成立的条件、实际问题等发现隐含信息作为条件,我们把这样的条件称为隐含条件,所以我们在做题时,要注意发现题目中的隐含条件.
阅读下面的解题过程,体会如何发现隐含条件并回答下面的问题.
化简:$(\sqrt{1-3 x})^2-|1-x|$ .
解:隐含条件为 $1-3 x \geq 0$ ,解得 $x \leq \frac{1}{3}$ ,
$$
\therefore 1-x>0 \text {, }
$$
$\therefore$ 原式 $=(1-3 x)-(1-x)=1-3 x-1+x=-2 x$ .
【启发应用】
(1)按照上面的解法,试化简:$\sqrt{(x-3)^2}-(\sqrt{2-x})^2$ ;
(2)已知 $a 、 b 、 c$ 为 $\triangle A B C$ 的三边长,化简:$\sqrt{(a-b-c)^2}+\sqrt{(b-a-c)^2}+\sqrt{(c-b-a)^2}$ .
阅读材料.
把根式 $\sqrt{x \pm 2 \sqrt{y}}$ 进行化简,若能找到两个数 $m 、 n$ ,是 $m^2+n^2=x$ 且 $m n=\sqrt{y}$ ,则把 $x \pm 2 \sqrt{y}$ 变成 $m^2+n^2 \pm 2 m m=(m \pm n)^2$ 开方,从而使得 $\sqrt{x \pm 2 \sqrt{y}}$ 化简.
如:$\sqrt{3+2 \sqrt{2}}=\sqrt{1+2 \sqrt{2}+2}=\sqrt{(\sqrt{1})^2+2 \times 1 \times \sqrt{2}+(\sqrt{2})^2}=\sqrt{(1+\sqrt{2})^2}=|1+\sqrt{2}|=1+\sqrt{2}$解答问题:
(1)填空:$\sqrt{5+2 \sqrt{6}}=$ $\_\_\_\_$ ,$\sqrt{7-4 \sqrt{3}}=$ $\_\_\_\_$ .
(2)$\sqrt{3-2 \sqrt{2}}+\sqrt{5-2 \sqrt{6}}+\sqrt{7-2 \sqrt{12}}+\sqrt{9-2 \sqrt{20}}$