单选题 (共 3 题 ),每题只有一个选项正确
设0<a<1,则随机变量X的分布列是
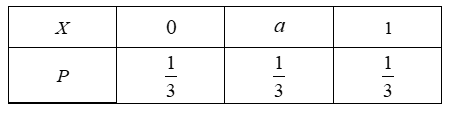
则当 $a$ 在 $(0,1)$ 内增大时,
$\text{A.}$ $D(X)$ 增大
$\text{B.}$ $D(X)$ 减小
$\text{C.}$ $D(X)$ 先增大后减小
$\text{D.}$ $D(X)$ 先减小后增大
某群体中的每位成员使用移动支付的概率都为 $p$ ,各成员的支付方式相互独立,设 $X$ 为该群体的 10 位成员中使用移动支付的人数,$D X=2.4, P(X=4) < P(X=6)$ ,则 $p=$
$\text{A.}$ 0.7
$\text{B.}$ 0.6
$\text{C.}$ 0.4
$\text{D.}$ 0.3
设随机变量X的概率分布列为

则 $P (| X -3|=1)$ 的值为
$\text{A.}$ $\frac{7}{12}$
$\text{B.}$ $\frac{5}{12}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{6}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
盒中有 4 个球,其中 1 个红球, 1 个绿球, 2 个黄球.从盒中随机取球,每次取 1 个,不放回,直到取出红球为止.设此过程中取到黄球的个数为 $\xi$ ,则 $P(\xi=0)=$ $\qquad$ ,$E(\xi)=$ $\qquad$ .
口袋内装有 10 个相同的球,其中 5 个球标有数字 0,5 个球标有数字1.若从袋中摸出 5 个球,则摸出的 5 个球所标数字之和小于 2 或大于 3 的概率是
一个袋子中有大小和质地相同的 5 个球,其中有 3 个红色球, 2 个白色球,从袋中不放回地依次随机摸出 2个球,则第 2 次摸到红色球的概率为
解答题 (共 14 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得 10 分,负方得 0 分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为 $0.5,0.4,0.8$ ,各项目的比赛结果相互独立.
(1)求甲学校获得冠军的概率;
(2)用 $X$ 表示乙学校的总得分,求 $X$ 的分布列与期望.
某学校组织"一带一路"知识竞赛,有 $A, B$ 两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束 $A$ 类问题中的每个问题回答正确得 20 分,否则得 0 分;$B$ 类问题中的每个问题回答正确得 80 分,否则得 0 分,已知小明能正确回答 $A$ 类问题的概率为 0.8 ,能正确回答 $B$ 类问题的概率为 0.6 ,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答 $A$ 类问题,记 $X$ 为小明的累计得分,求 $X$ 的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
设随机变量 X 的分布列 $P \left( X =\frac{ k }{5}\right)= ak ( k =1,2,3,4,5)$ .
(1)求常数 $a$ 的值;
(2)求 $P \left( X \geqslant \frac{3}{5}\right)$ ;
(3)求 $P \left(\frac{1}{10} < X < \frac{7}{10}\right)$ .
已知随机变量X的分布列如下表:
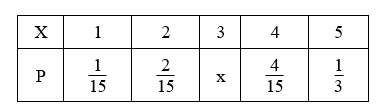
则实数 x 的值为 $\qquad$ , $P \left(\frac{2}{3} < x < \frac{9}{2}\right)=$ $\qquad$ ;
设X是一个离散型随机变量,其分布列为
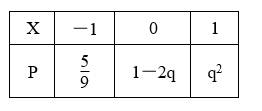
则 $q =$ $\qquad$ .
随机变量 $X$ 的分布列如下:
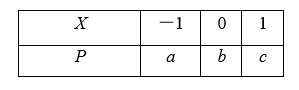
其中 $a, b, c$ 成等差数列,则 $P(|X|=1)=$ $\qquad$ ,公差 $d$ 的取值范围是
设离散型随机变量 $X$ 的分布列为
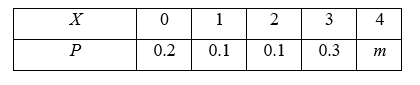
(1)求 $2 X+1$ 的分布列;
(2)求随机变量 $\eta=|X-1|$ 的分布列.
一机床生产了 100 个汽车零件,其中有 40 个一等品、 50 个合格品、 10 个次品,从中随机地抽出 4 个零件作为样本.用 $X$ 表示样本中一等品的个数.
(1)若有放回地抽取,求 $X$ 的分布列;
(2)若不放回地抽取,用样本中一等品的比例去估计总体中一等品的比例.
(1)求误差不超过 0.2 的 $X$ 的值;
(2)求误差不超过 0.2 的概率(结果不用计算,用式子表示即可)
某小组共 10 人,利用假期参加义工活动.已知参加义工活动次数为 $1,2,3$ 的人数分别为 3,3 , 4.现从这 10 人中随机选出 2 人作为该组代表参加座谈会.
(1)设事件 A 为"选出的 2 人参加义工活动次数之和为 4 ",求事件 A 发生的概率;
(2)设 X 为选出的 2 人参加义工活动次数之差的绝对值,求随机变量 X 的分布列和数学期望.
一批产品共 10 件,其中 7 件正品, 3 件次品,每次从这批产品中任取一件,在下列两种情况下,分别求直至取得正品时所需次数 X 的概率分布。
(1)每次取出的产品不再放回;
(2)每次取出的产品仍放回.
已知甲、乙、丙三个研究项目的成员人数分别为 $20,15,10$ .现采用分层抽样的方法从中抽取 9 人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个研究项目的成员中分别抽取多少人?
(2)若抽出的 9 人中有 4 人睡眠不足, 5 人睡眠充足,现从这 9 人中随机抽取 3 人做进一步的访谈调研,若随机变量 $X$ 表示抽取的 3 人中睡眠充足的成员人数,求 $X$ 的分布列与数学期望.
袋中有形状和大小相同的两个红球和三个白球,甲、乙两人依次不放回地从袋中摸出一球,后摸球的人不知前面摸球的结果,则乙摸出红球的概率是
中国载人航天工程办公室发布消息,为发挥中国空间站的综合效益,中国首个太空科普教育品牌"天宫课堂"正式推出.中国空间站首次太空授课活动于 2021年12月9日面向全球进行直播.为了了解学生对此次直播课的观看情况,现从高三某班随机选取 10 名学生进行调查,发现有 6 名学生观看了直播, 4 名学生未观看直播.
(1)若从这 10 名学生中任选 2 名学生,求至多有 1 名学生未观看直播的概率;
(2)若从这 10 名学生中任选 3 名学生,记其中观看了直播的学生人数为 $X$ ,求 $X$ 的分布列和数学期望.
由文化和旅游部会同国家体育总局共同编制的《滑雪旅游度假地等级划分》(以下简称《标准》)日前发布实施。《标准》的发布得到旅游业界的广泛关注,将有力推动我国冰雪旅游高质量发展,助力北京2022年冬奥会举办.为推广滑雪运动,某滑雪场开展滑雪促销活动.促销期间滑雪场的收费标准是:

不足 1 小时的部分按 1 小时计算.有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过 1 小时离开的概率分别为 $\frac{1}{4}, \frac{1}{6} ; 1$ 小时以上且不超过 2 小时离开的概率分别为 $\frac{1}{2}, \frac{2}{3}$ ,两人滑雪时间都不会超过 3 小时.
(1)求甲、乙两人所付的滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量 $X$ ,求 $N$ 的分布列和期望(结果用分数表示).