解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算积分 $\int_C e ^{|z|^2} \operatorname{Re} z d z$ ,其中 $C$ 为从 0 到 $1+ i$ 的直线段。
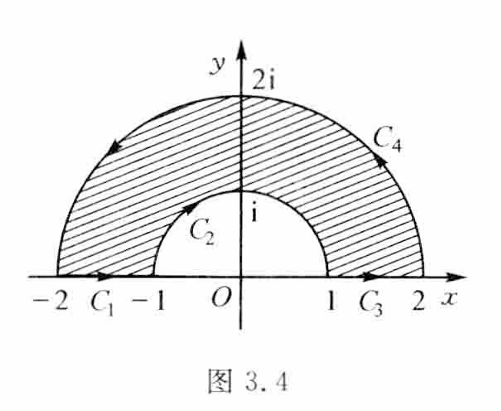
计算积分 $\oint_C \frac{z}{\bar{z}} d z$ ,其中 $C$ 为半圆环区域的正向边界,如图3.4所示.
算积分 $\int_C z \sin z d z$ ,其中 $C$ 为从 0 到 i 的任意路径。
$\oint_C \frac{d z}{z^2-a^2}, C:|z-a|=a$
$\oint_C \frac{d z}{\left(z^2+1\right)\left(z^2+4\right)}, C:|z|=\frac{3}{2}$
$\oint_C \frac{ e ^z}{\left(z+\frac{\pi}{2} i \right)^4} d z, C:|z|=3$
$\oint_C \frac{\cos z}{z\left(z-\frac{\pi}{2}\right)^3} d z, C:\left|z-\frac{\pi}{2}\right|=\frac{1}{4}$
(1)计算积分 $\oint_C \frac{2 z-1}{z^2-z} d z$ ,其中 $C$ 为包含 0 与 1 的任意正向简单闭曲线;
(2)计算积分 $\oint_C \frac{2 z+3}{z\left(z^2+1\right)} d z$ ,其中 $C:\left|z-\frac{ i }{2}\right|=1$ .
计算积分 $\oint_C \frac{|d z|}{|z-1|^2}, C:|z|=2$ .
求积分 $I=\oint_C \frac{1}{z^3(z+1)(z-2)} d z$ 的值,其中 $C$ 为 $|z|=r, r \neq 1,2$ .
证明题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设函数 $f(z)$ 与 $g(z)$ 在区域 $D$ 内处处解析,$C$ 为 $D$ 内的任何一条简单闭曲线,$C$ 的内部全含于区域 $D$ ,如果 $f(z)=g(z)$ 在 $C$ 上所有的点处成立.试证在 $C$ 内所有的点处 $f(z)=g(z)$ 也成立。