单选题 (共 3 题 ),每题只有一个选项正确
如图所示,虚线上方存在垂直纸面的匀强磁场(具体方向未知),磁感应强度大小为B,一比荷为k的带负电粒子从虚线上的M点垂直磁场方向射入磁场,经过一段时间,该粒子经过N点(图中未画出),速度方向与虚线平行向右,忽略粒子的重力.则下列说法正确的是
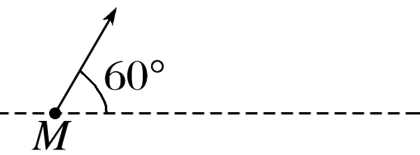
$\text{A.}$ 磁场的方向垂直纸面向外
$\text{B.}$ 粒子从M运动到N的时间为 $\pi/6kB$
$\text{C.}$ 如果N点到虚线的距离为L,则粒子在磁场中做圆周运动的半径为2L
$\text{D.}$ 如果N点到虚线的距离为L,则粒子射入磁场的速度大小为kBL
如图所示,abcd为边长为L的正方形,在四分之一圆abd区域内有垂直正方形平面向外的匀强磁场,磁感应强度大小为B.一个质量为m、电荷量为+q的带电粒子从b点沿ba方向射入磁场,粒子恰好能通过c点,不计粒子的重力,则粒子的速度大小为
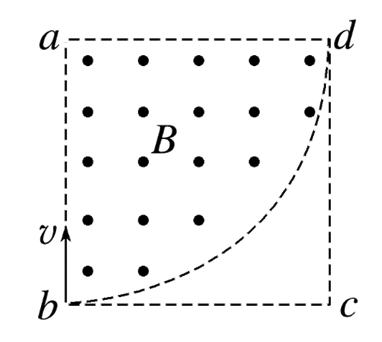
$\text{A.}$ $\frac{q B L}{m}$
$\text{B.}$ $\frac{\sqrt{2} q B L}{2 m}$
$\text{C.}$ $\frac{(\sqrt{2}-1) q B L}{m}$
$\text{D.}$ $\frac{(\sqrt{2}+1) q B L}{m}$
真空中有一匀强磁场,磁场边界为两个半径分别为a和2a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示.一电子以速率v沿半径方向射入磁场.已知电子质量为m,电荷量为e,忽略重力.为使电子不能进入内部无磁场区域,磁场的磁感应强度B最小为
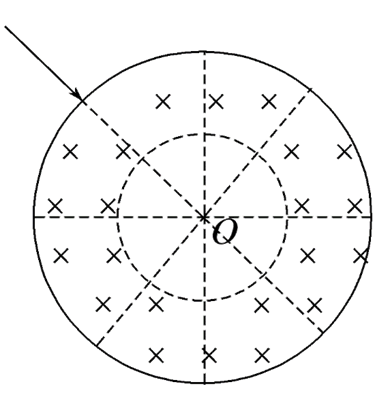
$\text{A.}$ $\frac{m v}{a e}$
$\text{B.}$ $\frac{2 m v}{3 a e}$
$\text{C.}$ $\frac{m v}{3 a e}$
$\text{D.}$ $\frac{m v}{2 a e}$
多选题 (共 6 题 ),每题有多个选项正确
粒子物理研究中使用的一种球状探测装置横截面的简化模型如图所示.内圆区域有垂直纸面向里的匀强磁场,外圆是探测器.两个粒子先后从P点沿径向射入磁场,粒子1沿直线通过磁场区域后打在探测器上的M点.粒子2经磁场偏转后打在探测器上的N点.装置内部为真空状态,忽略粒子重力及粒子间相互作用力.下列说法正确的是
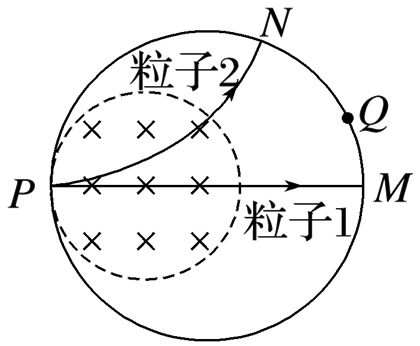
$\text{A.}$ 粒子1可能为中子
$\text{B.}$ 粒子2可能为电子
$\text{C.}$ 若增大磁感应强度,粒子1可能打在探测器上的Q点
$\text{D.}$ 若增大粒子入射速度,粒子2可能打在探测器上的Q点
如图所示,虚线MN上方存在匀强磁场,磁感应强度大小为B.一群电子以不同速率从边界MN上的P点以相同的入射方向射入磁场.其中某一速率为v的电子从Q点射出边界.已知电子入射方向与边界MN的夹角为θ,则
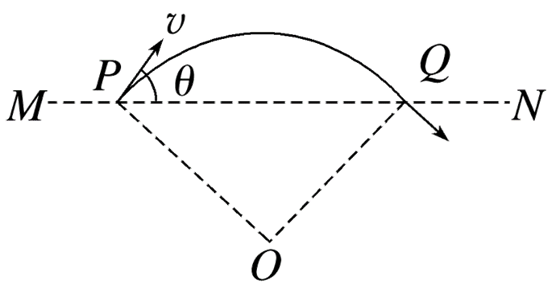
$\text{A.}$ 该匀强磁场的方向垂直纸面向里
$\text{B.}$ 所有电子在磁场中的轨迹半径相等
$\text{C.}$ 速率越大的电子在磁场中运动时间越长
$\text{D.}$ 在此过程中每个电子的速度方向都改变2θ
如图所示,A粒子和B粒子先后以同样大小的速度从宽度为d、方向垂直纸面向外的有界匀强磁场的边界上的O点,分别以与边界成37°和53°角的方向射入磁场,sin 37°=0.6,sin 53°=0.8,又都恰好垂直另一边界飞出,若粒子重力不计,则下列说法中正确的是

$\text{A.}$ A、B两粒子均带正电
$\text{B.}$ A、B两粒子在磁场中做圆周运动的半径之比是4∶3
$\text{C.}$ A、B两粒子比荷之比是4∶3
$\text{D.}$ A、B两粒子在磁场中做圆周运动的时间之比是53∶37
如图所示的虚线框为一正方形区域,该区域内有一垂直于纸面向里的匀强磁场,一带电粒子从a点沿与ab边成30°角方向射入磁场,恰好从b点飞出磁场;另一带电粒子以相同的速率从a点沿ad方向射入磁场后,从c点飞出磁场,不计重力,则两带电粒子的比荷之比及在磁场中的运动时间之比分别为

$\text{A.}$ $\frac{q_1}{m_1}: \frac{q_2}{m_2}=1: 1$
$\text{B.}$ $\frac{q_1}{m_1}: \frac{q_2}{m_2}=2: 1$
$\text{C.}$ $t_1: t_2=2: 3$
$\text{D.}$ $t_1: t_2=1: 3$
如图,在平面直角坐标系 $O x y$ 的第一象限内,存在垂直纸面向外的匀强磁场,磁感应强度大小为 $B$ .大量质量为 $m$ 、电量为 $q$ 的相同粒子从 $y$ 轴上的 $P(0, \sqrt{3} L)$ 点,以相同的速率在纸面内沿不同方向先后射入磁场,设入射速度方向与 $y$ 轴正方向的夹角为 $\alpha\left(0 \leqslant \alpha \leqslant 180^{\circ}\right)$ .当 $\alpha=150^{\circ}$ 时,粒子垂直 $x$ 轴离开磁场.不计粒子的重力.则
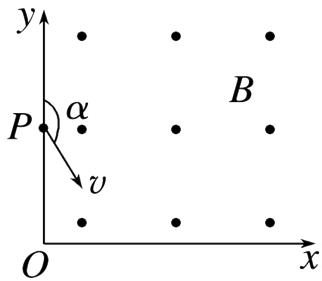
$\text{A.}$ 粒子一定带正电
$\text{B.}$ 当 $\alpha=45^{\circ}$ 时,粒子也垂直 $x$ 轴离开磁场
$\text{C.}$ 粒子入射速率为 $\frac{2 \sqrt{3} q B L}{m}$
$\text{D.}$ 粒子离开磁场的位置到 $O$ 点的最大距离为 $3 \sqrt{5} L$
速度均为 $v_0$ 的 ${ }_1^3 H$ 和 ${ }_2^4 He$ 的混合粒子流沿着与直径 $a b$ 夹角为 $\alpha(\alpha$ 角未知)的方向垂直进入圆柱形匀强磁场区域(未画出),一种粒子的出射方向恰与直径 $a b$ 平行向右,另一种粒子刚好从直径的另一点 $b$ 出射.已知元电荷为 $e$ ,${ }^3 H$的质量为 $3 m,{ }_2^4 He$ 的质量为 4 m ,不计粒子的重力和粒子间相互作用力,该区域的磁感应强度大小为 $B$ ,则
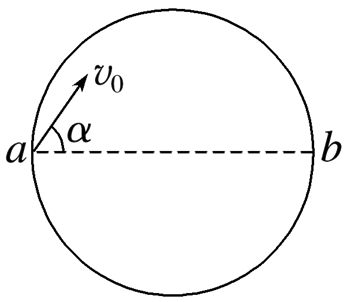
$\text{A.}$ 出射方向恰与直径 $a b$ 平行的粒子为 ${ }_2^4 He$
$\text{B.}$ ${ }_2^4 He$ 的速度偏转角是 ${ }_3^3 H$ 速度偏转角的 2 倍
$\text{C.}$ $\alpha=60^{\circ}$
$\text{D.}$ 磁场圆的半径为 $\frac{\sqrt{3} m v_0}{B e}$