单选题 (共 10 题 ),每题只有一个选项正确
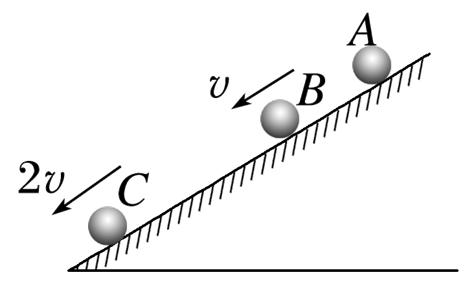
.如图所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则AB∶BC等于
$\text{A.}$ 1∶1
$\text{B.}$ 1∶2
$\text{C.}$ 1∶3
$\text{D.}$ 1∶4
汽车在平直的公路上行驶,发现险情紧急刹车,汽车立即做匀减速直线运动直到停止,已知汽车刹车时第1 s内的位移为13 m,最后1 s内的位移为2 m,则下列说法正确的是
$\text{A.}$ 汽车在第1 s末的速度可能为10 m/s
$\text{B.}$ 汽车加速度大小可能为3 m/s2
$\text{C.}$ 汽车在第1 s末的速度一定为11 m/s
$\text{D.}$ 汽车的加速度大小一定为4.5 m/s2
汽车在水平面上刹车,其位移与时间的关系是$x=24t-6t^2$ (m),则它在前3 s内的平均速度为
$\text{A.}$ 8 m/s
$\text{B.}$ 10 m/s
$\text{C.}$ 12 m/s
$\text{D.}$ 14 m/s
超音速巡航是指飞机在不开启后燃器的情况下能够持续在1.5倍音速以上进行超过30分钟的超音速飞行.超音速巡航的提出主要是基于快速突防的战术思想,因此,该技术在未来的超视距作战中具有很大的优势,超音速巡航是第五代战斗机的主要技术特征之一.某第五代战机在一次直线加速飞行中,速度由270 m/s提升至510 m/s,耗时一分钟,假设加速过程为匀加速运动,则该过程飞行的距离为

$\text{A.}$ 16 200 m
$\text{B.}$ 23 400 m
$\text{C.}$ 30 600 m
$\text{D.}$ 46 800 m
在2021年东京奥运会上,我国运动健儿摘金夺银,为国争光.其中在跳水男子 3 米板决赛中,我国选手谢思場夺得金牌!在某次比赛中,若将运动员入水后向下的运动视为匀减速直线运动,该运动过程的时间为 $8 t$ .设运动员入水后向下运动过程中,第一个 $t$ 时间内的位移大小为 $x_1$ ,最后两个 1 时间内的总位移大小为 $x_2$ ,则 $x_1: x_2$ 为
$\text{A.}$ $17: 4$
$\text{B.}$ 13 : 4
$\text{C.}$ 15 : 4
$\text{D.}$ 15 : 8
如图所示,一质点做匀加速直线运动先后经过 $A, ~ B, ~ C$ 三点,已知从 $A$ 到 $B$ 和从 $B$ 到 $C$ 速度的增加量 $\Delta v$ 均为 $6 m / s$ , $A B$ 间的距离 $x_1=3 m, ~ B C$ 间的距离 $x_2=13 m$ ,则该质点的加速度为
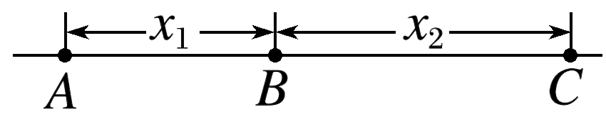
$\text{A.}$ $3.6 m / s ^2$
$\text{B.}$ $4 m / s ^2$
$\text{C.}$ $4.2 m / s ^2$
$\text{D.}$ $4.8 m / s ^2$
如图所示,一小球(可视为质点)以初速度 $10 m / s$ 从斜面底端 $O$ 冲上—固定斜面,$A, ~ B, ~ C$ 依次是斜面上的三个点,$A C$ 间距为 $8 m, ~ B$ 为 $A C$ 中点.小球经过 2 s 第一次通过 $A$ 点,又经 4 s第二次通过 $C$ 点,不计一切摩擦,则下列说法正确的是
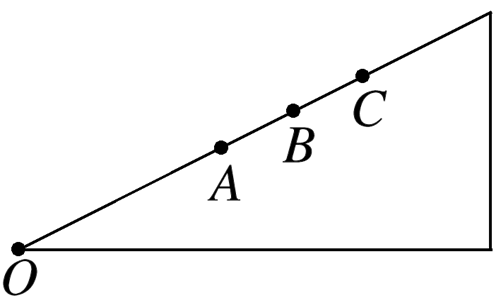
$\text{A.}$ 小球的加速度大小为 $3 m / s ^2$
$\text{B.}$ $O A$ 间距为 8 m
$\text{C.}$ 第一次通过 $B$ 点的速度大小一定为 $2 \sqrt{5} m / s$
$\text{D.}$ 第 3 s 末经过 $B$ 点
为了研究运动员起跑阶段的运动情况,用频率为2 Hz频闪照相机记录运动员起跑阶段不同时刻的位置,如图所示,用厘米刻度尺测量照片上运动员不同位置间的距离,已知照片与实物的尺寸比例为1∶50,运动员起跑阶段的运动可视为匀加速直线运动.下列说法正确的是

$\text{A.}$ 运动员起跑阶段的加速度为2 m/s2
$\text{B.}$ 运动员通过照片中3 cm位置时速 度为1 m/s
$\text{C.}$ 照片中0位置为运动员的起跑位置
$\text{D.}$ 运动员在照片前6 cm内的平均速度为4 m/s
高铁站台上, 5 位旅客在各自车厢候车线处候车,若动车每节车厢长均为 $l$ ,动车进站时做匀减速直线运动.站在 2 号候车线处的旅客发现 1 号车厢经过他所用的时间为 $t$ ,动车停下时该旅客刚好在 2 号车厢门口(2号车厢最前端),如图所示,则

$\text{A.}$ 动车从经过 5 号候车线处的旅客开始到停止运动,经历的时间为 $3 t$
$\text{B.}$ 动车从经过 5 号候车线处的旅客开始到停止运动,平均速度为 ${ }_t^l$
$\text{C.}$ 1 号车厢头部经过 5 号候车线处的旅客时的速度为 $\frac{4 l}{t}$
$\text{D.}$ 动车的加速度大小为 $\frac{l}{t^2}$
测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335 m,某时刻B发出超声波,同时A由静止开始做匀加速直线运动,当B接收到反射回来的超声波信号时,A、B相距355 m,已知声速为340 m/s,则汽车的加速度大小为

$\text{A.}$ 20 m/s2
$\text{B.}$ 10 m/s2
$\text{C.}$ 5 m/s2
$\text{D.}$ 无法确定
多选题 (共 1 题 ),每题有多个选项正确
一辆汽车以速度 $v_0$ 匀速行驶,司机观察到前方人行横道有行人要通过,于是立即刹车.从刹车到停止,汽车正好经过了 24 块规格相同的路边石,汽车刹车过程可视为匀减速直线运动.下列说法正确的是
$\text{A.}$ 汽车经过第 1 块路边石末端时的速度大小为 $\sqrt{\frac{23}{24}} v_0$
$\text{B.}$ 汽车经过第 18 块路边石末端时的速度大小为 $\frac{\sqrt{3}}{2} v_0$
$\text{C.}$ 汽车经过前 12 块路边石与后 12 块路边石的时间之比为 $1: \sqrt{2}$
$\text{D.}$ 汽车经过前 18 块路边石与后 6 块路边石的时间之比为 $1: 1$
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
ETC 是不停车电子收费系统的简称.最近,某ETC通道的通行车速由原来的 $20 km / h$ 提高至 $40 km / h$ ,车通过ETC通道的流程如图所示.为简便计算,假设汽车以 $v_0=30 m / s$ 的速度朝收费站沿直线匀速行驶,如过ETC通道,需要在收费站中心线前 $d=10 m$ 处正好匀减速至 $v_1=4 m / s$ ,匀速通过中心线后,再匀加速至 $v_0$ 正常行驶.设汽车匀加速和匀减速过程中的加速度大小均为 $1 m / s ^2$ ,忽略汽车车身长度.

(1)求汽车过ETC通道时,从开始减速到恢复正常行驶过程中的位移大小;
(2)如果汽车以v2=10 m/s的速度通过匀速行驶区间,其他条件不变,求汽车提速后过收费站过程中比提速前节省的时间.