解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
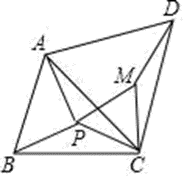
如图,在 $\triangle {ABC}$ 中, P 为平面内一点,连结 $ {PA}, {PB}, {PC}$ ,分别以 PC 和 AC 为一边向右作等边三角形 $\triangle {PCM}$ 和 $\triangle {ACD}$ .
【探究】求证: $ {PM}= {PC}, {MD}= {PA}$
【应用】若 $ {BC}= {a}, {AC}= {b}, \angle {ACB}=60^{\circ}$ ,则 $ {PA}+ {PB}+ {PC}$ 的最小值是 $\_\_\_\_$ (用 $ {a}, {b}$表示)
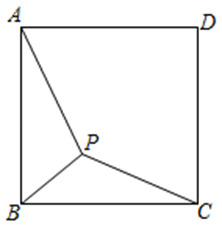
如图,$P$ 为正方形 $A B C D$ 内的动点,若 $A B=2$ ,则 $P A+P B+P C$ 的最小值为
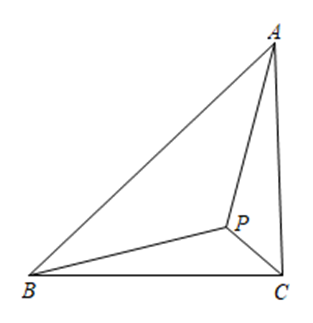
如图,$\triangle A B C$ 中,$\angle B A C=45^{\circ}, A B=6, A C=4, P$ 为平面内一点,求 $2 \sqrt{2} B P+\sqrt{5} A P+3 P C$ 最小值
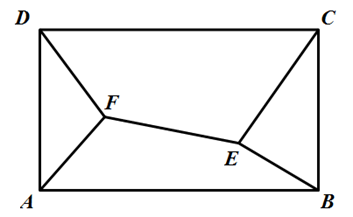
如图,$A B C D$ 为矩形,$A B=4 \sqrt{3}, A D=4, E F$ 为 $A B C D$ 内两点,求 $(A F+D F+F E +C E+B E)$ 的最小值.
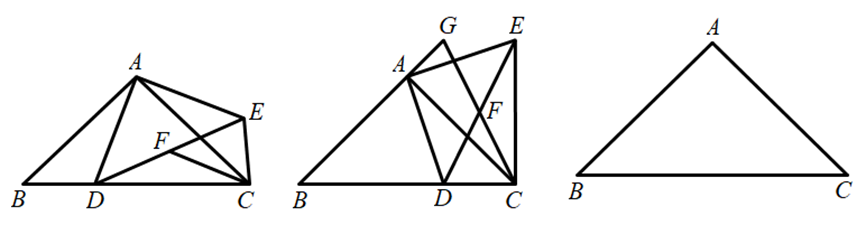
如图,在 Rt $\triangle A B C$ 中,$\angle B A C=90^{\circ}, A B=A C$ ,点 $D$ 是 $B C$ 边上一动点,连接 $A D$ ,把 $A D$ 绕点 $A$ 逆时针旋转 $90^{\circ}$ ,得到 $A E$ ,连接 $C E, D E$ .点 $F$ 是 $D E$ 的中点,连接 $C F$ .
(1)求证:$C F=\frac{\sqrt{2}}{2} A D$ ;
(2)如图 2 所示,在点 $D$ 运动的过程中,当 $B D=2 C D$ 时,分别延长 $C F, B A$ ,相交于点 $G$ ,猜想 $A G$ 与 $B C$ 存在的数量关系,并证明你猜想的结论;
(3)在点 $D$ 运动的过程中,在线段 $A D$ 上存在一点 $P$ ,使 $P A+P B+P C$ 的值最小.当 $P A+P B+P C$ 的值取得最小值时,$A P$ 的长为 $m$ ,请直接用含 $m$ 的式子表示 $C E$ 的长.