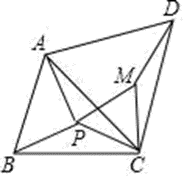
如图，在 $\triangle {ABC}$ 中， P 为平面内一点，连结 $ {PA}, {PB}, {PC}$ ，分别以 PC 和 AC 为一边向右作等边三角形 $\triangle {PCM}$ 和 $\triangle {ACD}$ ．
【探究】求证： $ {PM}= {PC}, {MD}= {PA}$
【应用】若 $ {BC}= {a}, {AC}= {b}, \angle {ACB}=60^{\circ}$ ，则 $ {PA}+ {PB}+ {PC}$ 的最小值是 $\_\_\_\_$ （用 $ {a}, {b}$表示）