某机构为了解市民对交通的满意度，随机抽取了 100 位市民进行调查结果如下：回答＂满意＂的人数占总人数的一半，在回答＂满意＂的人中，＂上班族＂的人数是＂非上班族＂人数的 $\frac{3}{7}$ ；在回答＂不满意＂的人中，＂非上班族＂占 $\frac{1}{5}$ ．
（1）请根据以上数据填写下面 $2 \times 2$ 列联表，并依据小概率值 $\alpha=0.001$ 的独立性检验，分析能否认为市民对于交通的满意度与是否为上班族存关联？


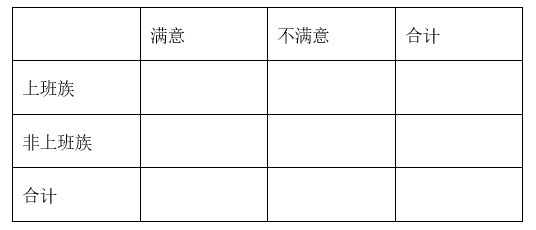
（2）为了改善市民对交通状况的满意度，机构欲随机抽取部分市民做进一步调查．规定：抽样的次数不超过 $n\left(n \in N _{+}\right)$，若随机抽取的市民属于不满意群体，则抽样结束；若随机抽取的市民属于满意群体，则继续抽样，直到抽到不满意市民或抽样次数达到 $n$ 时，抽样结束．
（i）若 $n=5$ ，写出 $X_5$ 的分布列和数学期望；
（ii）请写出 $X_n$ 的数学期望的表达式（不需证明），根据你的理解说明 $X_n$ 的数学期望的实际意义．附：

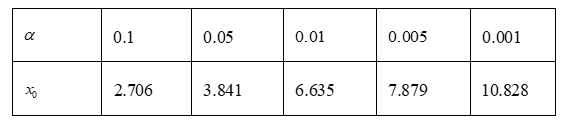
参考公式：$\quad \chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ，其中 $n=a+b+c+d$ ．