单选题 (共 5 题 ),每题只有一个选项正确
某企业为了解员工身体健康情况,采用分层抽样的方法从该企业的营销部门和研发部门抽取部分员工体检,已知该企业营销部门和研发部门的员工人数之比是 $4: 1$ ,且被抽到参加体检的员工中,营销部门的人数比研发部门的人数多 72 ,则参加体检的人数是( )
$\text{A.}$ 90
$\text{B.}$ 96
$\text{C.}$ 120
$\text{D.}$ 144
我国西北某地区开展改造沙漠的巨大工程,该地区对近5年投入的沙漠治理经费x(亿元)和沙漠治理面积y(万亩)的相关数据统计如下表所示.

根据表中所给数据,得到 $y$ 关于 $x$ 的线性回归方程为 $\hat{y}=2 x+a$ ,则 $a=()$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
每年的毕业季都是高校毕业生求职和公司招聘最忙碌的时候,甲、乙两家公司今年分别提供了2个和3个不同的职位,一共收到了100份简历,具体数据如下:
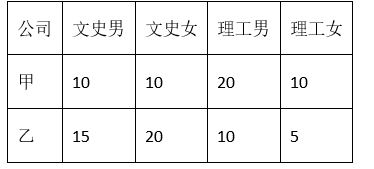
分析毕业生的选择意愿与性别的关联关系时,已知对应的 $K^2$ 的观测值 $k_1 \approx 1.010$ ;分析毕业生的选择意愿与
专业关联的 $K^2$ 的观测值 $k_2 \approx 9.090$ ,则下列说法正确的是( )
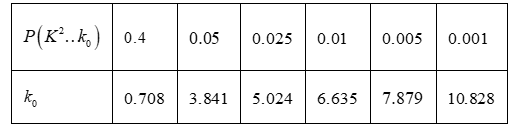
$\text{A.}$ 有 $99.9 \%$ 的把握认为毕业生的选择意愿与专业相关联
$\text{B.}$ 毕业生在选择甲、乙公司时,选择意愿与专业的关联比与性别的关联性更大一些
$\text{C.}$ 理科专业的学生更倾向于选择乙公司
$\text{D.}$ 女性毕业生更倾向于选择甲公司
为加强居民对电信诈骗的认识,提升自我防范的意识和能力,拧紧保障居民的生命财产的“安全阀”,某社区开展了“防电信诈骗进社区,筑牢生命财产防线”专题讲座,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份防电信诈骗手段知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图所示,则
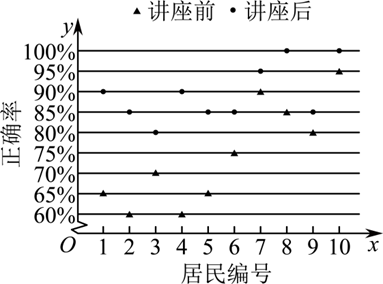
$\text{A.}$ 讲座前问卷答题的正确率的中位数大于75%
$\text{B.}$ 讲座后问卷答题的正确率的众数为85%
$\text{C.}$ 讲座前问卷答题的正确率的方差小于讲座后正确率的方差
$\text{D.}$ 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
某车间从生产的一批产品中随机抽取了 1000 个零件进行一项质量指标的检测,整理检测结果得此项质量指标的频率分布直方图如图所示,则下列结论错误的是( )
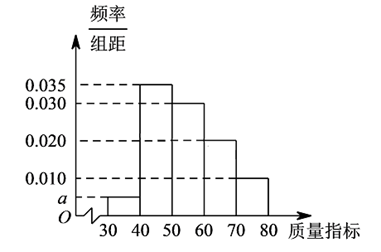
$\text{A.}$ $a=0.005$
$\text{B.}$ 估计这批产品该项质量指标的众数为 45
$\text{C.}$ 估计这批产品该项质量指标的中位数为 60
$\text{D.}$ 从这批产品中随机选取 1 个零件,其质量指标在 $[50,70)$ 的概率约为 0.5
多选题 (共 3 题 ),每题有多个选项正确
已知一组数据: $0,1,2,4$ ,则下列各选项正确的是
$\text{A.}$ 该组数据的极差,中位数,平均数之积为 10
$\text{B.}$ 该组数据的方差为 2.1875
$\text{C.}$ 从这 4 个数字中任取 2 个不同的数字可以组成 8 个两位数
$\text{D.}$ 在这 4 个数字中任取 2 个不同的数字组成两位数,从这些两位数中任取一数,取得偶数的概率为 $\frac{7}{9}$
已知某产品的单价 $x$ 以及销量 $y$ 情况统计如下表所示,由表中数据求得经验回归方程 $\hat{y}=-4 x+\hat{a}$ ,则下列说法正确的是
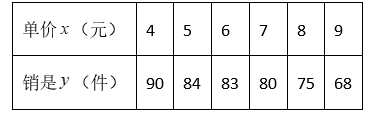
$\text{A.}$ 销量的平均数为 80 件
$\text{B.}$ 根据经验回归方程可以测得,单价每上升 1 元,销量就减少 4 件
$\text{C.}$ $\hat{a}=26$
$\text{D.}$ 根据经验回归方程可以预测,单价为 10 元时,销量为 66 件
某校高三一名数学教师从该校高三学生中随机抽取男、女生各50名进行了身高统计,得到男、女身高分别近似服从正态分布N(173,11)和N(164,9),并对其是否喜欢体育锻炼进行数据统计,得到如下2×2列联表:
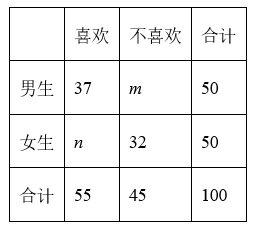
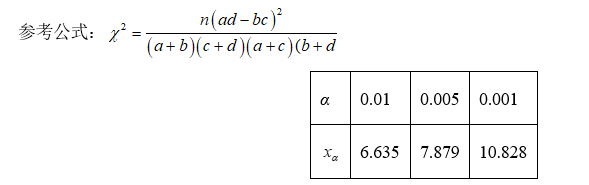
则下列说法正确的是
$\text{A.}$ $m=13, n=18$
$\text{B.}$ 男生身高的平均数约为 173 ,女生身高的平均数约为 164
$\text{C.}$ 男生身高的标准差约为 11 ,女生身高的标准差约为 9
$\text{D.}$ 依据 $\alpha=0.01$ 的独立性检验,认为喜欢体育锻炼与性别有关联
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
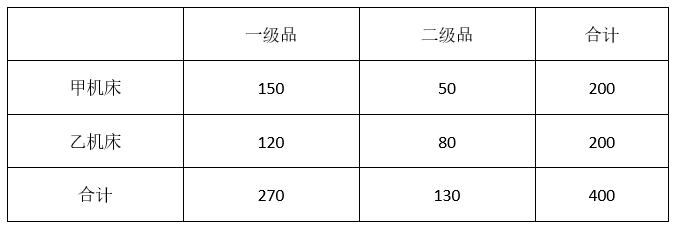
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
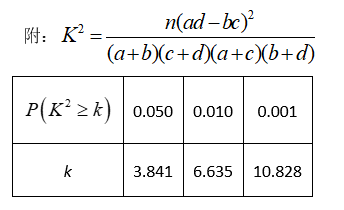
某机构为了解市民对交通的满意度,随机抽取了 100 位市民进行调查结果如下:回答"满意"的人数占总人数的一半,在回答"满意"的人中,"上班族"的人数是"非上班族"人数的 $\frac{3}{7}$ ;在回答"不满意"的人中,"非上班族"占 $\frac{1}{5}$ .
(1)请根据以上数据填写下面 $2 \times 2$ 列联表,并依据小概率值 $\alpha=0.001$ 的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存关联?
(2)为了改善市民对交通状况的满意度,机构欲随机抽取部分市民做进一步调查.规定:抽样的次数不超过 $n\left(n \in N _{+}\right)$,若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到 $n$ 时,抽样结束.
(i)若 $n=5$ ,写出 $X_5$ 的分布列和数学期望;
(ii)请写出 $X_n$ 的数学期望的表达式(不需证明),根据你的理解说明 $X_n$ 的数学期望的实际意义.附:
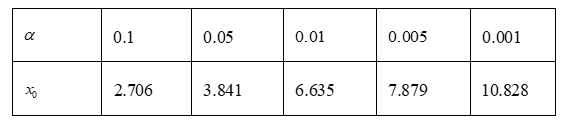
参考公式:$\quad \chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .