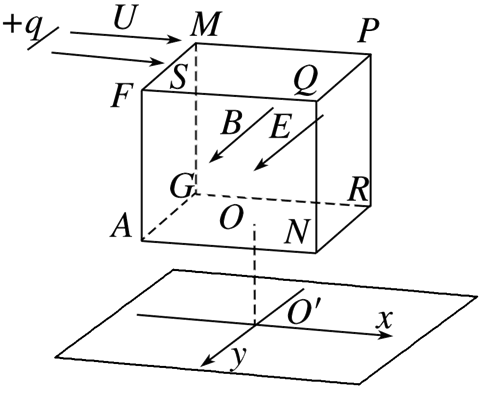
如图所示，一些质量为 $m$ 、电荷量为 $+q$ 的带电粒子从一线状粒子源射出（初速度可视为 0 ），经过电压为 $U$ 的电场加速后，粒子以一定的水平初速度从 $M S$ 段垂直射出（ $S$ 为 $M F$ 中点），进入棱长为 $L$ 的正方体电磁修正区内（内部有垂直面 $M P R G$ 的方向如图，磁感应强度 $B$ 和电场强度 $E$ 大小未知的匀强磁场与匀强电场）。距离正方体底部 $\sqrt{3} L$ 处有一与 $R N A G$ 平行且足够大平板。现以正方体底面中心 $O$ 在平板的垂直投影点为原点，在平板内建立直角坐标系（其中 $x$ 轴与 $G R$ 平行）。所有带电粒子都从正方体底面离开，且从 $M$点进入正方体的粒子在正方体中运动的时间满足 $\frac{2 \pi m}{3 q B}$ ．不计粒子重力．



(1)求粒子进入棱长为L的正方体电磁修正区时速度的大小；
(2)粒子射出正方体电磁修正区后到达平板所需的时间；
（3）若满足关系式 $E=\sqrt{\frac{q U B^2}{2 \pi^2 m}}$ ，求从 $M$ 点入射的粒子最后打到平板上的位置坐标．（结果用 $L$ 表示）