单选题 (共 1 题 ),每题只有一个选项正确
2021年中国全超导托卡马克核聚变实验装置创造了新的纪录.为粗略了解等离子体在托卡马克环形真空室内的运动状况,某同学将一小段真空室内的电场和磁场理想化为方向均水平向右的匀强电场和匀强磁场(如图),电场强度大小为 $E$ ,磁感应强度大小为 $B$ .若某电荷量为 $q$ 的正离子在此电场和磁场中运动,其速度平行于磁场方向的分量大小为 $v_1$ ,垂直于磁场方向的分量大小为 $v_2$ ,不计离子重力,则
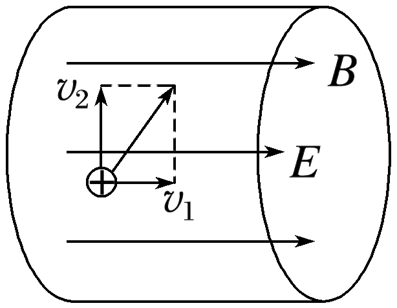
$\text{A.}$ 电场力的瞬时功率为 $q E \sqrt{v_1{ }^2+v_2{ }^2}$
$\text{B.}$ 该离子受到的洛伦兹力大小为 $q v_1 B$
$\text{C.}$ $v_2$ 与 $v_1$ 的比值不断变大
$\text{D.}$ 该离子的加速度大小不变
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示,坚直平面 $M N R S$ 的右侧存在方向坚直向上且足够大的匀强磁场,从平面 $M N R S$ 上的 $O$ 点处以初速度 $v_0=10 m / s$ 垂直MNRS面向右抛出一带电荷量为 $q$ 、质量为 $m$ 的小球.若磁感应强度大小 $B=\frac{\pi m}{q}, ~ g$ 取 $10 m / s ^2$ .求:
(1)小球离开磁场时的速度大小;
(2)小球离开磁场时的位置与抛出点的距离.

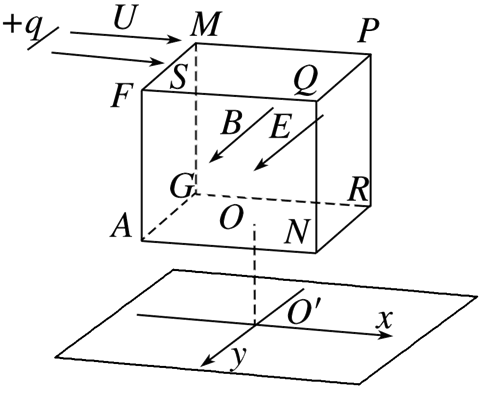
如图所示,一些质量为 $m$ 、电荷量为 $+q$ 的带电粒子从一线状粒子源射出(初速度可视为 0 ),经过电压为 $U$ 的电场加速后,粒子以一定的水平初速度从 $M S$ 段垂直射出( $S$ 为 $M F$ 中点),进入棱长为 $L$ 的正方体电磁修正区内(内部有垂直面 $M P R G$ 的方向如图,磁感应强度 $B$ 和电场强度 $E$ 大小未知的匀强磁场与匀强电场)。距离正方体底部 $\sqrt{3} L$ 处有一与 $R N A G$ 平行且足够大平板。现以正方体底面中心 $O$ 在平板的垂直投影点为原点,在平板内建立直角坐标系(其中 $x$ 轴与 $G R$ 平行)。所有带电粒子都从正方体底面离开,且从 $M$点进入正方体的粒子在正方体中运动的时间满足 $\frac{2 \pi m}{3 q B}$ .不计粒子重力.
(1)求粒子进入棱长为L的正方体电磁修正区时速度的大小;
(2)粒子射出正方体电磁修正区后到达平板所需的时间;
(3)若满足关系式 $E=\sqrt{\frac{q U B^2}{2 \pi^2 m}}$ ,求从 $M$ 点入射的粒子最后打到平板上的位置坐标.(结果用 $L$ 表示)