如图所示，在坚直平面内的直角坐标系 $x O y$ 中，第四象限内有垂直坐标平面向里的匀强磁场和沿 $x$ 轴正方向的匀强电场，磁感应强度大小为 $B$ ，电场强度大小为 $E$ 。第一象限中有沿 $y$ 轴正方向的匀强电场（电场强度大小未知），且某未知矩形区域内有垂直坐标平面向里的匀强磁场（磁感应强度大小也为 $B$ ）。一个带电小球从图中 $y$ 轴上的 $M$ 点沿与 $x$ 轴成 $\theta=45^{\circ}$ 角斜向上做匀速直线运动，由 $x$ 轴上的 $N$ 点进入第一象限并立即在矩形磁场区域内做匀速圆周运动，离开矩形磁场区域后垂直打在 $y$ 轴上的 $P$ 点（图中未标出），已知 $O 、 N$ 两点间的距离为 $L$ ，重力加速度大小为 $g$ ，取 $\sin 22.5^{\circ}=0.4, ~ \cos 22.5^{\circ}=0.9$ ．求：



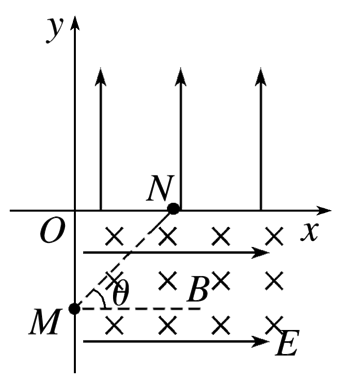
(1)小球所带电荷量与质量的比值和第一象限内匀强电场的电场强度大小；
(2)矩形匀强磁场区域面积S的最小值；
(3)小球从M点运动到P点所用的时间.